Una iniziativa del dipartimento di Matematica per avvicinare tutti gli ambiti di ricerca e ricordarci che la matematica è unica ed interconnessa.
Un mercoledì al mese, il dipartimento si riunisce per conoscere e far conoscere le persone dietro la matematica:
docenti, ricercatori e assegnisti presentano le loro tematiche di ricerca in maniera sintetica e accessibile.
Seguiranno tè e biscotti... non dimenticare di portare la tua tazza da tè!
Organizza Prof.ssa Elisabetta Scoppola, con la partecipazione dei dottorandi in Matematica.
Iscriviti o visualizza il calendario degli eventi.
Prossimo evento
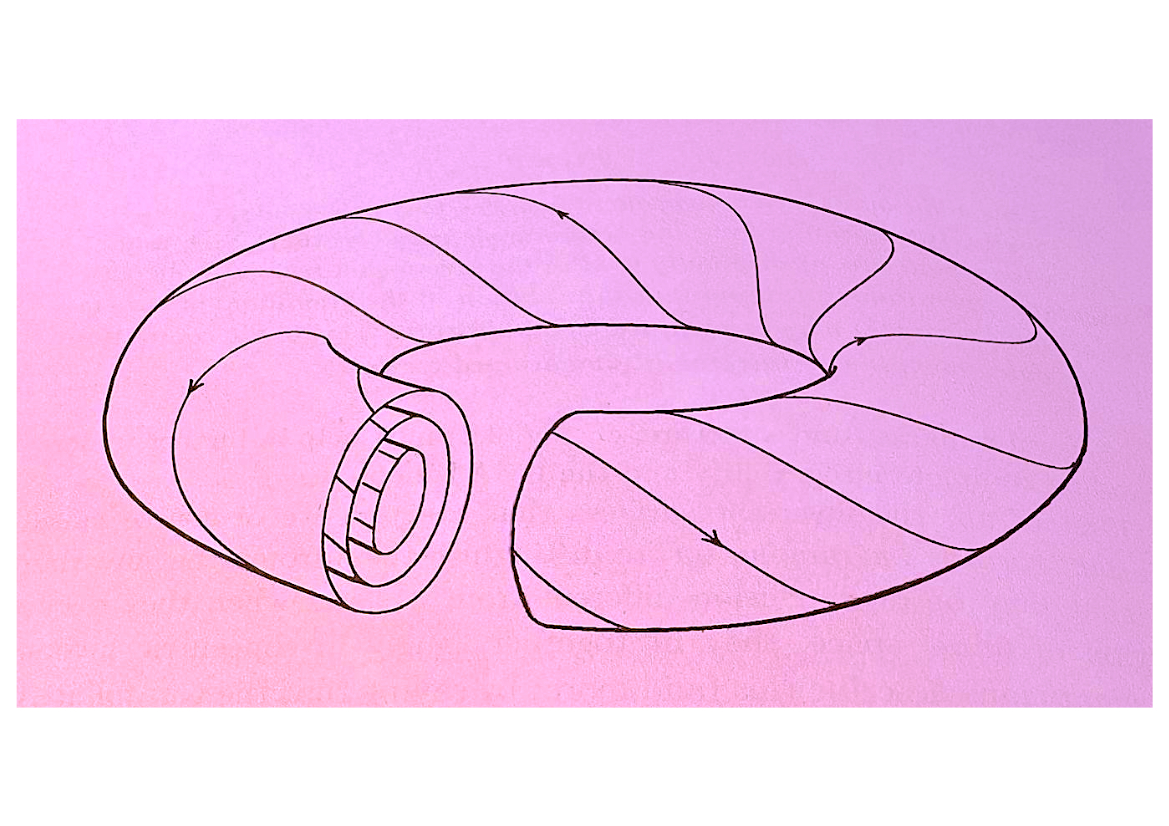
The Kolmogorov set in Hamiltonian dynamics
Di Luigi Chierchia
10 dicembre 2025 – ore 16:00 – Aula M1
Abstract. In frictionless phenomena, such as planetary dynamics, regular motions (periodic and quasi-periodic) have been observed and studied since ancient times (Ptolemy). In particular, in the nineteenth century, mathematicians and astronomers engaged in an intense debate over the convergence of formal power-series expansions of quasi-periodic solutions of nearly integrable systems (for example, Poincaré was convinced of their generic divergence, while Weierstrass argued in favour of convergence). A crucial step was taken by Kolmogorov in 1954, when he proved convergence of such series (under suitable assumptions) and stated (without proof) that the set of quasi-periodic solutions of a general nearly integrable Hamiltonian system (the “Kolmogorov set”) fills compact regions of its phase space up to a small exceptional set, whose Lebesgue measure tends to zero as the perturbation parameter goes to zero. The main question then becomes: what is, generically, the asymptotic measure of the Kolmogorov set (as the perturbation parameter goes to zero)? In this Tè di matematica seminar, I will discuss, in general terms, some of these issues, from their (modern) origins up to the research frontier.

An Introduction to the Mathematical Theory of Anderson Localization
Di Fabio Martinelli
29 Ottobre 2025 – ore 16:00 – Aula M1
Abstract. In 1958, the physicist P. W. Anderson published the paper "Absence of Diffusion in Certain Random Lattices," which contributed to winning him the Nobel Prize in 1977 for the discovery of the phenomenon now known as "Anderson localization." In the simplest case, Anderson localization states that a Schroedinger operator with a random potential on, e.g., a \(d\)-dimensional lattice has a pure-point spectrum with exponentially localized eigenstates if the randomness of the potential is sufficiently strong. In his Nobel lecture Anderson said "...Localization was a different matter: very few believed it at the time, and even fewer saw its importance; among those who failed to fully understand it at first was certainly its author. It has yet to receive adequate mathematical treatment, and one has to resort to the indignity of numerical simulations to settle even the simplest questions about it." Proving Anderson localization was one of the great problems in mathematical physics in the early 1980s, and E. Scoppola greatly contributed to its solution in the hard case \(d > 1\). On the occasion of her retirement, I will provide a brief overview of the Anderson model and eigenfunction localization, as well as some of the more recent developments. If time allows, I will also try to describe how the basic multiscale analysis underlying the proof of Anderson localization can be applied to other, quite different, contexts.
Eventi Futuri
Eventi passati

Tropicalizing curves and divisors
Di Margarida Melo
4 giugno 2025 – ore 16:00 – Aula M3
Abstract.
In algebraic geometry, understanding the geometry of degenerations of fundamental objects as curves is of central importance in the study of the initial objects themselves.
However, dealing with degenerated objects is often hard from the point of view of the combinatorial data one has to handle.
In the last few years, a very sucessful approach to handle degeneration data has been to use tools from tropical geometry.
Indeed, it is often the case that by tropicalizing algebro-geometric objects, one gets a modular way to describe degeneration data, which can then be treated as moduli spaces themselves.
This interplay between degenerated algebro-geometric objects and their tropical counterparts has led to incredible developments in our current understanding of the geometry of both.
In the talk, I will try to explain these ideas in the case of curves and divisors on curves. In particular, I will illustrate the tropical version of the Rieman-Roch theorem and how to use specialization techniques to prove a number of results in classical algebraic geometry via their tropical/combinatorial counterparts.

The friendship paradox for social networks
Di Frank den Hollander (Leiden University)
7 maggio 2025 – ore 16:00 – Aula M3
Abstract.
Consider a group of individuals who form a social network. For each individual in the group, compute the difference between the average number of friends of its friends and the number of its friends (all friendships are mutual), and average these numbers over all the individuals in the group. It turns out that the latter average is always non-negative, and is strictly positive as soon as not all individuals have exactly the same number of friends. This bias, which at first glance seems counterintuitive, goes under the name of friendship paradox, even though it is a hard fact. In this talk we model the social network as a graph and explain where the bias comes from. For two examples of random graphs we show how the bias can be quantified.
Based on joint work with R.S. Hazra and A. Parvaneh.
Continued fractions: introduction and applications
Di Laura Capuano
26 marzo 2025 – ore 16:00 – Aula M3
Abstract. The continued fraction expansion of a real number \(\alpha\) is a very efficient tool for finding the best rational approximation of \(\alpha\). Moreover, continued fractions occur both in many theoretical questions in number theory, complex analysis, dynamical systems, as well as in more practical questions related for example to cryptography. After giving an introduction to the classical theory of continued fractions in the field of real numbers and to famous results and open problems in this setting, I will explain how this theory can be generalized to other worlds, for example to the field of \(p\)-adic numbers, where many differences with the classical case arise.
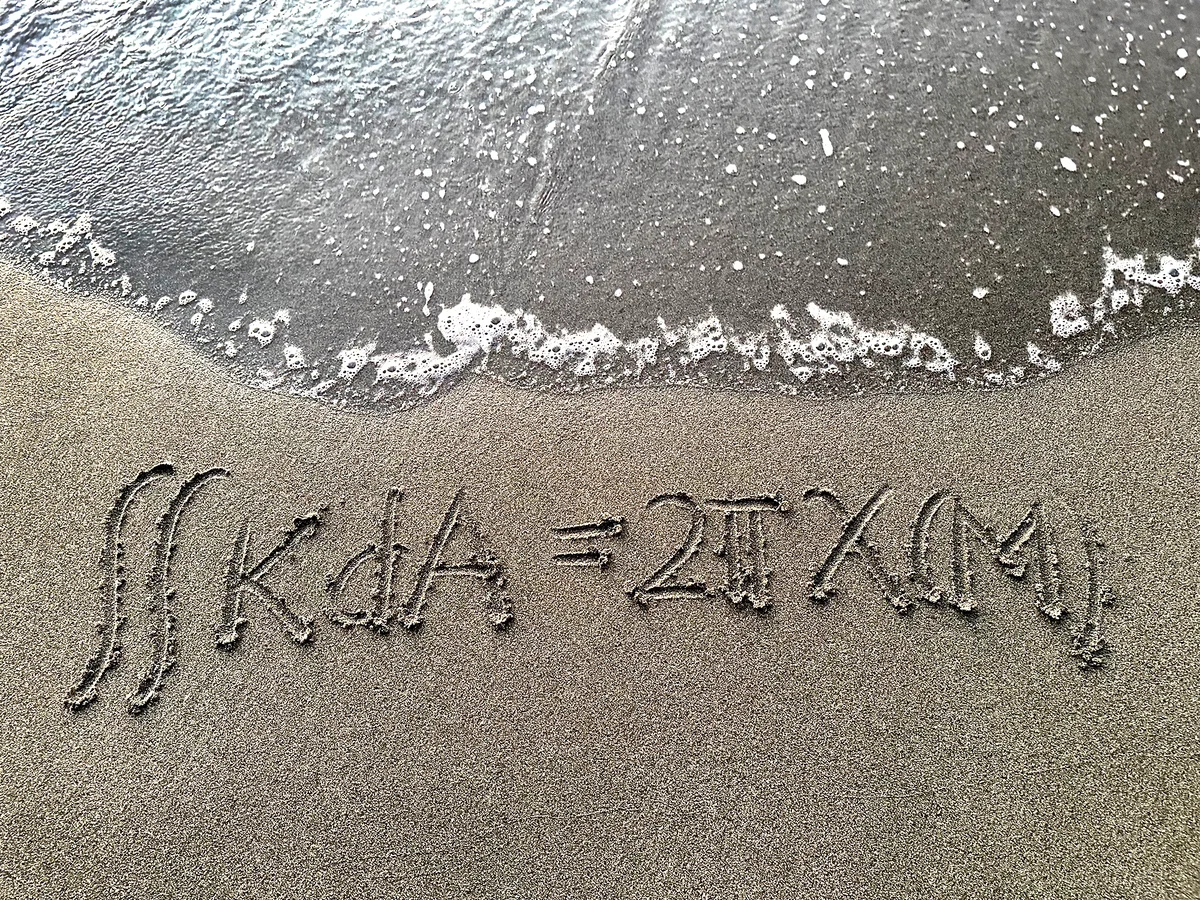
Curvature of a surface and partial differential equations
Di Luca Battaglia
19 febbraio 2025 – ore 16:00 – Aula M3
Abstract. In this talk I will describe the problem of prescribing Gaussian curvature on compact surfaces, namely: given a smooth function on a surface, deform the surface so that the Gaussian curvature at any point coincides with the given function. I will then talk about the generalization of this problem to surfaces with boundary or with singular points. Such problems, in principle purely geometric, actually have a totally equivalent formulation in terms of partial differential equations, which I will discuss in the second part of the talk.

Playing games with random rules
Di Matteo Quattropani
08 gennaio 2025 – ore 16:00 – Aula M1
Abstract. Game theory is a branch of applied mathematics that deals with models of strategic interaction between rational (and often selfish) agents. Since the pioneering work of Von Neumann and Nash, mathematical game theory has primarily focused on existential results for various notions of equilibrium (i.e., solution), aiming to categorize games into classes for which such equilibria exist. It is somewhat surprising how little attention has been paid to the “average-case approach”, in which the focus shifts to the frequency according to which equilibria exist, i.e., on their typicality. In this context, random games—where the payoffs are randomly sampled—provide a natural starting point for analysis. In this talk, after introducing some fundamental concepts at the heart of game theory, I will present both classic and more recent results on random games. Along the way, I will highlight key takeaways that mathematicians and economists could get out of such results.

Recurrent motions in Hamiltonian dynamics
Di Livia Corsi
27 novembre 2024 – ore 16:00 – Aula M1
Abstract. Besides few well-known exceptions, time evolutions can be very unpredictable, even when restricting to Hamiltonian dynamics, where in fact recurrent and chaotic dynamics are known to coexist. However many physically relevant systems can be described as a perturbation of some integrable Hamiltonian evolution and one hopes that, at least in this case, some more information can be obtained.

The mathematics of gases of quantum particles in 1 dimension
Di Robin Reuvers
29 maggio 2024 – ore 16:00 – Aula M3
Abstract. I will try to give a very basic introduction to the mathematical study of gases of quantum particles, focusing on one-dimensional systems. A large part of the talk will be devoted to motivation and some background on classical and quantum mechanics. Towards the end, I will discuss some of my own work.

Solitari e dispersivi: una (non troppo breve) passeggiata tra le onde
Di Roberto Feola
24 aprile 2024 – ore 16:00 – Aula M3
Abstract. La propagazione delle onde in mezzi dispersivi è descritta da un gran numero di equazioni alle derivate parziali, come l'equazione di Schrödinger (NLS), l'equazione delle onde (NLW), le equazioni di Eulero dell'idrodinamica e i numerosi modelli che da essa derivano. Le equazioni non lineari si usano per descrivere comportamenti complessi con coesistenza di moti ordinati o caotici a seconda dei dati iniziali o delle condizioni al contorno. Lo studio di queste equazioni pone alcune domande fondamentali che hanno ispirato un intero campo di ricerca negli ultimi anni: su che scala di tempo le soluzioni non lineari restano vicino a quelle lineari? Quali nuovi fenomeni compaiono per effetto della non linearità? Esiste un comportamento "tipico" delle soluzioni? Se si, per quanto tempo persiste? I risultati ottenuti valgono anche in caso di piccole perturbazioni o modifiche del dato iniziale? Durante il tè discuteremo alcuni di questi problemi con particolare interesse a fenomeni di stabilità per soluzioni del problema delle onde d’acqua.

I matematici giocano... a biliardo!
Di Alfonso Sorrentino
25 marzo 2024 – ore 16:00 – Aula M3
Abstract. Questo seminario si propone di esplorare il mondo affascinante dei "biliardi matematici", concentrandosi in particolare sulla classe dei cosiddetti "Biliardi di Birkhoff". Questi biliardi presentano tavoli di gioco costituiti da regioni del piano limitate, strettamente convessi e con bordi regolari (ma senza "buche"). Le proprietà dinamiche di questi modelli matematici sono strettamente legate alla forma del tavolo che si considera: comprendere fino a che punto la conoscenza di certi aspetti dinamici permetta di ricostruire la forma del tavolo è alla centro di importanti congetture che alimentano intense attività di ricerca. Durante il seminario, esamineremo alcune di queste questioni e presenteremo i più recenti contributi verso la loro risoluzione.

Diversità filogenetica e geometria delle configurazioni di punti
Di Luca Schaffler
21 febbraio 2024 – ore 16:00 – Aula M3
Abstract. Gli alberi filogenetici in biologia illustrano le relazioni evolutive tra diverse specie. La distanza evolutiva tra coppie di specie può essere registrata in un vettore chiamato vettore di dissimilarità. Durante il tè, esploreremo la geometria dell'insieme dei vettori di dissimilarità, portando a una nuova variante pesata di questi che si comporta meglio nella stima degli alberi filogenetici da dati su insiemi arbitrari di specie anziché solo coppie. Al tempo stesso, scopriremo connessioni inaspettate tra la filogenetica, la geometria tropicale, e le configurazioni di punti su determinati tipi di curve. I risultati originali presentati sono in collaborazione con Alessio Caminata, Noah Giansiracusa, e Han-Bom Moon.

Pausa natalizia

Modelli matematici microscopici e macroscopici per i movimenti pedonali
Di Emiliano Cristiani (IAC–CNR)
13 dicembre 2023 – ore 16:00 – Aula M1
Abstract. Come si descrive matematicamente la dinamica delle folle? E a cosa serve saperla prevedere? In questo seminario passeremo in rassegna gli approcci più usati per descrivere il movimento dei pedoni, per poi concentrarci su due modelli recenti: il primo è un approccio microscopico (agent-based) non differenziale in grado di simulare la dinamica pedonale anche ad altissime densità; il secondo invece è un approccio macroscopico fluidodinamico basato sulla teoria dei giochi di campo medio.

Conduttività e coefficienti di trasporto in sistemi quantistici a molti corpi
Di Alessandro Giuliani
22 novembre 2023 – ore 16:00 – Aula M1
Abstract. L'obiettivo della meccanica statistica è il calcolo delle leggi macroscopiche dei corpi a partire dalle leggi di interazioni microscopiche tra i costituenti elementari del sistema. Un esempio estremamente importante anche per le recenti applicazioni ai nanomateriali è il calcolo delle leggi della conduzione elettrica di un sistema (e in particolare della sua caratterizzazione come isolante, conduttore o semiconduttore) a partire dalla struttura reticolare microscopica del materiale e dalle proprietà chimico/fisiche dei suoi ioni. Dopo aver definito la nozione di conduttività elettrica di un sistema a molti corpi nell'approssimazione lineare (conduttività Kubo) sia nel caso classico che quantistico, accennerò a come affrontare il calcolo di tale quantità e farò una breve panoramica su alcuni risultati recenti sulla conduttività di bassa temperatura in sistemi di elettroni interagenti in una e due dimensioni.

Contare oggetti aritmetici
Di Fabrizio Barroero
11 ottobre 2023 – ore 16:00 – Aula M3
Abstract.
Quantificare il numero di oggetti con una data proprietà in una certa famiglia è un problema che appare praticamente in ogni ambito della matematica e la teoria dei numeri non fa eccezione.
Per esempio, Gauss si interessò molto alla distribuzione dei numeri primi e congetturò che il numero di numeri primi minori di un dato intero \(x\) è circa \(\frac{x}{\log(x)}\).
Un altro problema affrontato da Gauss è il cosiddetto “problema del cerchio di Gauss”: quanti sono i punti a coordinate intere contenuti in un cerchio nel piano cartesiano? Più in generale, dato un sottoinsieme di uno spazio reale, è spesso utile capire quanti siano i punti a coordinate intere che esso contiene. Dopo aver enunciato un risultato ottenuto in collaborazione con Martin Widmer, parlerò di alcune applicazioni alla geometria aritmetica.

Pausa estiva

Reti abeliane, criticalità auto organizzata e modelli
Di Elisabetta Candellero
21 giugno 2023 – ore 16:00 – Aula 009
Abstract. Una rete è un sistema di processori collegati tra loro che ricevono in input un messaggio (scritto tramite un alfabeto noto) e producono un output che verrà inviato agli altri processori. La rete è abeliana quando ogni processore soddisfa delle condizioni per cui l'output finale non dipende dall'ordine dei caratteri processati. La proprietà di criticalità auto-organizzata, invece, è propria di sistemi di particelle che tendono a organizzarsi autonomamente per raggiungere uno stato "abbastanza stabile". Questi fenomeni sono di fondamentale importanza sia dal punto di vista teorico che delle applicazioni; durante il tè descriveremo alcune loro connessioni, esplorando esempi ed applicazioni interessanti nella matematica e al di fuori di essa, discutendo anche alcuni risultati recenti.

Geometria Diofantea: Numeri, equazioni, curve e forme geometriche
Di Amos Turchet
31 maggio 2023 – ore 16:00 – Aula M3
Abstract. Uno dei problemi più antichi in matematica è lo studio di equazioni polinomiali. Aggiungendo la semplice richiesta che le soluzioni delle equazioni siano numeri razionali o interi, domande che hanno classicamente risposte facili diventano improvvisamente incredibilmente sottili. Nell'arco del 1900 si è assistito a una "geometrizzazione" di questi problemi che ha portato a importanti risultati tra i quali la dimostrazione di Faltings della congettura di Mordell (medaglia Fields 1986) e ad applicazioni impreviste (crittosistemi ellittici o codici correttori). Durante il tè daremo un'introduzione ai problemi principali dell'area, evidenziando i suoi legami con la geometria e l'analisi complessa, fino ad alcuni sviluppi recenti.

Algoritmi naturali, computazioni emergenti
Di Vincenzo Bonifaci
29 marzo 2023 – ore 16:00 – Aula M3
Abstract. Come riesce la muffa mucillaginosa Physarum polycephalum a trovare il cammino più breve in un labirinto, e in generale a costruire reti sorprendentemente efficienti? Illustreremo il concetto di algoritmo naturale, dando una panoramica di come si possa analizzare matematicamente il meccanismo biofisico che consente ad un organismo acellulare di risolvere il problema del cammino minimo in un grafo. Discuteremo inoltre ulteriori problemi computazionali risolubili con algoritmi ispirati dalla natura.

