Elementi di Matematica: Insiemi, numeri e successioni
| Autore | Marco Falconi |
| Data | 2020-10-19 16:40:59 |
| Serie | Questa lezione è parte di una serie. Lista Prossima -> |
| Letture Addizionali | Matematica per le scienze della vita |
| Metadata | Scritto usando html-export e org-spec su emacs org-mode |
1 Sommario
In questa lezione introdurremo brevemente alcuni dei concetti base della matematica. Partiremo dal concetto di insieme, che useremo come punto di partenza per definire i numeri naturali. Definiti i numeri naturali e le loro principali proprietà, passeremo alla definizione dei numeri razionali e dei numeri reali (tramite i tagli di Dedekind). Infine, introdurremo il concetto di successione numerica, e di limite di una successione.
2 Insiemi
2.1 Definizione
Gli insiemi sono il concetto alla base della matematica moderna, e rappresentano delle collezioni di oggetti (che sono tipicamente accomunati da qualcosa). Un esempio tipico può essere l'insieme costituito dagli studenti iscritti al primo anno del corso di laurea in matematica dell'Università di Roma Tre. In matematica gli insiemi sono definiti a livello assiomatico come gli oggetti di base della teoria degli insiemi, su cui si sviluppano tutte le branche della matematica. Innanzitutto è necessario supporre che almeno un insieme esista. Questo fatto deve essere preso per vero, ovvero sarà un assioma della teoria. Per questioni di convenienza, nella formulazione più comune della teoria degli insiemi si pone come assioma che esista un insieme con un numero infinito di elementi. Per i nostri scopi ci limiteremo però a supporre che esista l'insieme vuoto (la sua esistenza è una conseguenza dell'assioma di esistenza di un insieme infinito, e del cosiddetto "schema di assiomi di separazione").
Chiameremo insieme vuoto, denotato dal simbolo \(\varnothing \), l'insieme che non contiene alcun elemento.
Dato l'insieme vuoto, possiamo costruire in maniera ricorsiva alcuni insiemi speciali con un numero finito di elementi. A tale proposito è conveniente introdurre la seguente notazione: denoteremo l'insieme \(S\) contenente gli elementi \(a,b,c,d\) tramite la notazione
\begin{equation} S=\{a,b,c,d\}\; . \end{equation}Abbiamo usato le parentesi graffe "\(\{\)" e "\(\}\)" per collezionare gli elementi dell'insieme \(S\). Adottiamo la regola di non ripetere mai, all'interno di un insieme, lo stesso elemento due volte. Per cui \(\{a,a,b,c\}\) non denota correttamente l'insieme \(\{a,b,c\}\). L'ordine in cui gli elementi dell'insieme vengono collezionati all'interno delle parentesi graffe è indifferente, per cui \(\{a,b,c,d\}\) e \(\{d,c,b,a\}\) denotano lo stesso insieme.
Scrivere tramite la notazione con parentesi graffe l'insieme vuoto \(\toggle{\texttip{\varnothing}{Cliccando qui è possibile visualizzare la soluzione} }{\textcolor{Red}{\text{Soluzione:}\, \varnothing =\{\: \}}}\endtoggle\).
Un'osservazione molto importante è la seguente: gli insiemi possono essere a loro volta elementi di un (altro) insieme. In particolare, nella teoria matematica degli insiemi, gli insiemi sono l'unico oggetto possibile: ogni insieme è collezione di altri insiemi. Per cui, se \(S\) è un insieme con 5 elementi, possiamo costruire l'insieme \(\{S\}\) che ha però un elemento solo (\(S\) per l'appunto). Ecco che allora questa idea ci fornisce un modo naturale di costruire ricorsivamente insiemi con \(0,1,2,3,\dotsc\) elementi (che devono essere tra loro distinti) a partire dall'insieme vuoto:
\begin{align} &\varnothing\\ &\{\varnothing\}\\ &\{\varnothing,\{\varnothing\}\}\\ &\bigl\{\varnothing , \{\varnothing\}, \{\varnothing, \{\varnothing\}\}\bigr\}\\ &\dotsc \end{align}Lo schema di ricorrenza è chiaro: dato un'insieme, costruiamo quello successivo aggiungendo agli elementi di quello dato esso stesso, come elemento. Per cui, chiaramente, se l'insieme dato aveva \(n\) elementi, quello successivo ne avrà uno in più. Questa costruzione ci tornerà utile nella §3 per definire i numeri naturali.
2.2 Relazioni e Operazioni fra insiemi
Definiamo ora alcune relazioni e operazioni fra insiemi.
Siano \(s,S\) due insiemi. Scriviamo \(s\in S\), ovvero \(s\) appartiene a \(S\) se \(s\) è un elemento dell'insieme \(S\), ovvero:
\begin{equation*} S=\{a,b,\dotsc,s,\dotsc\}\; . \end{equation*}La negazione di \(\in \) si scrive \(\notin\) (ovvero \(s\notin S\) significa che \(s\) non è elemento di \(S\)).
Siano \(S,T\) due insiemi. Essi si dicono uguali, \(S=T\) se e solo se hanno gli stessi identici elementi.
La negazione di \(=\) si scrive \(\neq\).
Siano \(S,T\) due insiemi. \(S\subseteq T\), ovvero \(S\) è un sottoinsieme di \(T\), se e solo se ciascun elemento di \(S\) è anche un elemento di \(T\).
Scriviamo invece \(S\subset T\), ovvero \(S\) è un sottoinsieme proprio di \(T\), se \(S\subseteq T\) e \(S\neq T\).
I concetti definiti sopra sono di comprensione piuttosto immediata, e non necessitano approfondimenti particolari. Si noti però che la nozione di appartenenza può portare a situazioni paradossali, che però sono escluse dagli assiomi della teoria. L'esempio più famoso è il seguente.
Si consideri la collezione
\begin{equation*} C=\{c\,,\, c\notin c\}\;. \end{equation*}Tale collezione porta ad un paradosso. Infatti la domanda "\(C\in C\)?" porta ad una contraddizione sia che abbia risposta positiva o negativa:
- se \(C\in C\), allora per definizione di \(C\) significa che \(C\notin C\), il che contraddice l'ipotesi;
- se \(C\notin C\), allora per definizione di \(C\) significa che \(C\in C\), il che contraddice l'ipotesi.
Il paradosso è dovuto al fatto che \(C\) è definito collezionando tutti i possibili oggetti che hanno una data proprietà. La teoria matematica degli insiemi perciò autorizza solamente la collezione di tutti gli oggetti appartenenti ad un certo insieme e che hanno una data proprietà. Nel caso in considerazione noi siamo quindi autorizzati solamente a considerare insiemi del tipo
\begin{equation*} C=\{c\in K\,,\, c\notin c\}\; , \end{equation*}dove \(K\) è un certo insieme dato. Chiaramente \(C\subseteq K\), ma a priori non è detto che \(C\) sia in \(K\) o meno. A questo punto il paradosso non sussiste più, infatti:
- è possibile che \(C\in C\), a patto che \(C\notin K\),
- è possibile che \(C\notin C\), a patto che \(C\notin K\);
ed in particolare è possibile che una sola delle due opzioni sia vera senza incorrere in contraddizioni.
Questa restrizione è quindi fondamentale per evitare le situazioni paradossali dovute al fatto di voler costruire degli insiemi "troppo grandi". Come ultima curiosità si noti che la collezione di tutti i possibili insiemi è decisamente troppo grande per essere un insieme, ed è infatti esclusa dalla restrizione appena introdotta (la sua definizione comporterebbe situazioni paradossali completamente analoghe a quella appena descritta).
Passiamo ora ad introdurre alcune operazioni fra insiemi: l'unione \(\cup \), l'intersezione \(\cap \), la differenza \(\smallsetminus \), la differenza simmetrica \(\Delta\), e il prodotto cartesiano \(\times\).
Siano \(S,T\) due insiemi. \(S\cup T\), ovvero l'unione di \(S\) e \(T\), è l'insieme che ha come elementi tutti e soli gli elementi sia di \(S\) che di \(T\):
\begin{equation*} S\cup T = \bigl\{s\,,\, s\in S \text{ oppure } s\in T\bigr\}\; . \end{equation*}Si noti che \(S\subseteq (S\cup T)\) e \(T\subseteq (S\cup T)\). In particolare \(S\cup T\) è l'insieme con meno elementi che contiene sia \(S\) che \(T\), e che \(S\cup T\) è vuoto se e solo se \(S=T=\varnothing \).
Siano \(S,T\) due insiemi. \(S\cap T\), ovvero l'intersezione di \(S\) e \(T\), è l'insieme che ha come elementi tutti e soli gli elementi in comune fra \(S\) e \(T\):
\begin{equation*} S\cap T =\bigl\{ s\, ,\, s\in S \text{ e } s\in T\bigr\}\; . \end{equation*}Si noti che \((S\cap T)\subseteq S\) e \((S\cap T)\subseteq T\). In particolare \(S\cap T\) è l'insieme con più elementi che è contenuto sia in \(S\) che in \(T\); inoltre \(S\cap T=\varnothing \) se e solo se \(S\) e \(T\) non hanno elementi comuni.
Siano \(S,T\) due insiemi. \(S\smallsetminus T\), ovvero la differenza insiemistica di \(S\) e \(T\) è l'insieme che come elementi tutti e soli gli elementi di \(S\) che non appartengono a \(T\):
\begin{equation*} S\smallsetminus T =\bigl\{s\in S\,,\, s\notin T\bigr\}\; . \end{equation*}Se \(T\subseteq S\) allora \(S\smallsetminus T\) è spesso chiamato il complementare di \(T\) in \(S\), e si usa la notazione \(T^{\mathrm{c}}\) (il fatto che il complementare sia preso in \(S\) è sottinteso).
Siano \(S,T\) due insiemi. \(S\Delta T\), ovvero la differenza simmetrica di \(S\) e \(T\) è l'insieme che come elementi tutti e soli gli elementi di \(S\) e \(T\) che non appartengono a \(S\cap T\):
\begin{equation*} S\Delta T= (S\cup T)\smallsetminus (S\cap T)\; . \end{equation*}Per definire il prodotto cartesiano di due insiemi, definiamo prima il concetto di coppia ordinata. Dati due oggetti \(a,b\), definiamo la coppia ordinata \((a,b)\) come l'insieme
\begin{equation} \label{eq:7} (a,b)= \{\{a\},\{a,b\}\}\; . \end{equation}Questa definizione ci permette di distinguere l'ordine in cui \(a\) e \(b\) vengono collezionati, contrariamente al semplice insieme \(\{a,b\}\) in cui come abbiamo discusso l'ordine in cui collezioniamo gli elementi è indifferente.
Siano \(S,T\) due insiemi. \(S\times T\), ovvero il prodotto cartesiano di \(S\) e \(T\) è l'insieme delle coppie ordinate in cui il primo elemento appartiene a \(S\) ed il secondo a \(T\), ovvero:
\begin{equation*} \label{eq:8} S\times T = \{(s,t)\, ,\, s\in S \text{ e } t\in T\}\; . \end{equation*}Gli elementi di un prodotto cartesiano di insiemi sono dunque "compositi", consistendo delle coppie ordinate di elementi dei due insiemi che lo formano. Ovviamente ne risulta che \(S\times T \neq T\times S\). Si osservi anche che \(S\times \varnothing = \varnothing \times S= \varnothing \) (infatti non è possibile formare coppie ordinate se uno dei due insiemi non ha nessun elemento).
2.3 Connettivi e Quantificatori logici
Nella sezione precedente abbiamo utilizzato, implicitamente e in maniera naturale, degli strumenti logici atti a connettere o quantificare le frasi matematiche.
Le frasi matematiche sono delle stringhe di simboli a cui è possibile assegnare un valore di verità, ovvero che possono essere o vere o false. I connettivi logici permettono di combinare fra loro delle frasi matematiche, ottenendo una nuova frase composita il cui valore di verità dipende da quello delle componenti e dall'azione del connettivo. Definiamo ora i tre connettivi fondamentali: e (\(\land\)), oppure (\(\vee\)), non (\(\neg\)). Il loro significato è lo stesso che si usa nel linguaggio comune, e non necessita quindi di chiarimenti particolari.
Siano \(A,B\) due frasi. \(\land\) è il connettivo tale per cui \(A\land B\) è vera se e solo se sia \(A\) che \(B\) sono vere.
Siano \(A,B\) due frasi. \(\vee\) è il connettivo tale per cui \(A\vee B\) è vera se e solo se \(A\) e \(B\) non sono entrambe false.
Sia \(A\) una frase. \(\neg\) è il connettivo tale per cui \(\neg A\) è vera se e solo se \(A\) è falsa.
Combinando i connettivi fondamentali è possibile ottenere altri connettivi, i più importanti sono le implicazioni logiche \(\longrightarrow\) e \(\longleftrightarrow\). Intuitivamente \(A\longrightarrow B\) significa che la frase \(B\) è implicata dalla frase \(A\), ovvero se \(A\) è vera, allora \(B\) è vera anch'essa. Si osservi che ciò comporta che se \(B\) è falsa, allora \(A\) dev'essere anch'essa falsa (perché?). \(A \longleftrightarrow B\) significa che sia \(A\longrightarrow B \) che \(B\longrightarrow A\), ovvero per quanto appena discusso che \(A\) è vera se e solo se anche \(B\) lo è. La definizione delle implicazioni utilizzando i connettivi fondamentali è la seguente:
\begin{align} &A\longrightarrow B = (\neg A)\vee B\; ,\\ &A \longleftrightarrow B = ((\neg A)\vee B) \land ((\neg B)\vee A)\; . \end{align}Oltre ai connettivi, giocano un ruolo altrettanto importante i quantificatori logici. Come la parola suggerisce, essi servono a quantificare delle frasi matematiche in cui appaiano delle variabili. Infatti, come si è detto in precedenza, le frasi matematiche sono stringhe di simboli che possono essere o vere o false. Questi simboli possono essere dei connettivi, delle costanti (ad esempio il numero 2 – che definiremo presto – o l'insieme vuoto \(\varnothing \)), oppure delle variabili. Le variabili sono simboli che a differenza delle costanti non hanno un valore preciso, ma possono variare per formare frasi differenti, e possono essere quantificate. Nella teoria degli insiemi, le variabili saranno degli insiemi generici, a cui non abbiamo ancora assegnato un valore preciso. Una variabile non quantificata si dice libera. Per convenienza, si esplicitano le variabili libere all'interno di una frase: scriveremo \[ A(x_1,x_2,\dotsc,x_n)\] per denotare una frase che ha come variabili libere \(x_1,\dotsc, x_n\). Una frase senza variabili libere è detta proposizione. I quantificatori logici sono due: esiste \(\exists \), e per ogni \(\forall \).
Sia \(A(x)\) una frase con variabile libera \(x\). Allora la frase
\begin{equation*} \exists x A(x) \end{equation*}non ha variabili libere (è una proposizione), e significa che esiste almeno un valore della variabile \(x\) – chiamiamolo \(\underline{x}\) per convenienza – per cui \(A(\underline{x})\) è vera.
Sia \(A(x)\) una frase con variabile libera \(x\). Allora la proposizione
\begin{equation*} \forall x A(x) \end{equation*}significa che per qualsiasi valore assunto dalla variabile \(x\) la frase \(A(x)\) è vera.
Si osservi che l'azione dei quantificatori vincola una variabile, ovvero ogni quantificatore elimina una variabile libera dalla frase considerata.
Si riscrivano le frasi e proposizioni matematiche nella precedente §2.2 utilizzando i connettivi e i quantificatori logici.
3 Numeri
I numeri sono alla base dell'indagine matematica, in particolare se applicata all'investigazione dei fenomeni naturali. Definire in maniera rigorosa i numeri è un'operazione semplice ma non banale, come vedremo in questa sezione. Dato che ciascuna tipologia di numero è utilizzata per definire quella successiva procediamo con ordine: si parte dai numeri naturali, per poi passare agli interi, ai razionali, e ai reali (discuteremo i numeri complessi in seguito). Sebbene saranno queste le uniche tipologie di numeri che considereremo, non sono però le uniche: chi fosse bramoso di conoscenza, potrà dare ampio sfogo a tale brama divertendosi con i numeri ordinali, cardinali, surreali, \(p\)-adici, e tanti altri.
3.1 Numeri Naturali
Partiamo con il concetto di numero naturale. Abbiamo introdotto nella §2 la teoria degli insiemi, da cui abbiamo detto si sviluppa tutta la matematica moderna. Ebbene anche il concetto di numero trova la sua formalizzazione nella teoria degli insiemi. I numeri naturali non sono altro che alcuni insiemi speciali, che peraltro abbiamo già visto.
Definiamo i numeri \(0,1,2,3\) come gli insiemi:
\begin{align*} &0= \varnothing \; ,\\ &1= \{\varnothing\}\; ,\\ &2= \{\varnothing ,\{\varnothing\}\}\; ,\\ &3= \bigl\{\varnothing ,\{\varnothing\}, \{\varnothing,\{\varnothing\}\}\bigr\}\; . \end{align*}In altre parole i primi quattro numeri non sono altro che gli insiemi con zero, uno, due, tre elementi rispettivamente, costruiti a partire dall'insieme vuoto. Tutti gli altri numeri naturali si possono costruire ricorsivamente allo stesso modo, semplicemente unendo al numero precedente (che è un insieme) l'insieme contenete il numero stesso come unico elemento (sempre inteso come insieme). Abbiamo quindi la seguente definizione:
Ciascun numero naturale \(n\) si definisce ricorsivamente a partire dallo zero tramite la relazione:
\begin{align*} &0=\varnothing \\ &\dotsc\\ &n= (n-1) \cup \{n-1\}\; . \end{align*}In altre parole,
\begin{equation*} n=\{0,1,\dotsc,n-1\}\; . \end{equation*}È conveniente introdurre una operazione \(\mathfrak{S}\), chiamata successivo che agisce sui numeri naturali nel modo seguente:
\begin{equation} \mathfrak{S}(n)= n \cup \{n\}\; . \end{equation}Per cui possiamo dire che \(0\) è l'unico numero naturale che non è successivo di nessun altro numero, e ogni numero \(n\) gode della proprietà
\begin{equation} \label{eq:0} n= \mathfrak{S}^n(0)= \underbrace{\mathfrak{S}(\mathfrak{S}(\mathfrak{S}(\mathfrak{S}\dotsc(\mathfrak{S}}_n(0))\dotsc)))\; , \end{equation}con la convenzione che \(\mathfrak{S}^0\) significa che applichiamo l'operazione successivo zero volte.
I numeri naturali, data la loro costruzione successiva, possono essere totalmente ordinati in modo ovvio.
Siano \(n,m\) due numeri naturali. Allora \[m < n\] se e solo se \(m \subset n\). In altre parole, \(m < n\) se e solo se esiste un numero naturale \(j\neq 0\) tale che \[n=\mathfrak{S}^j(m)\; .\]
Siano \(n,m\) due numeri naturali. Allora \[m\leq n\] se e solo se \(m \subseteq n\). In altre parole, \(m\leq n\) se e solo se esiste un numero naturale \(j\) tale che \[n=\mathfrak{S}^j(m)\; .\]
La definizione di \( > , \geq \) è perfettamente analoga, invertendo l'ordine dei due numeri considerati. La relazione \(\leq \) (o analogamente \(\geq\)) definisce un ordine totale, ovvero dati \(n,m\in \mathbb{N}\) qualsiasi, o \(n\leq m\) o \(m\leq n\) è vera (ed entrambe sono vere se e solo se \(n=m\)).
La collezione di tutti i numeri naturali è un insieme, che chiamiamo \(\mathbb{N}\). L'insieme \(\mathbb{N}\) contiene un numero infinito di elementi, infatti si può applicare l'operazione successivo un numero arbitrariamente grande di volte, ottenendo sempre un altro numero naturale. Possiamo quindi rappresentare i numeri naturali come una successione orientata di punti, collegati dall'operazione di prendere il successivo; solitamente si adotta la convenzione di orientarli in modo che crescano muovendosi verso destra:

Figura 1: Rappresentazione grafica di \(\mathbb{N}\)
3.1.1 Operazioni fra numeri naturali
Si possono definire alcune operazioni sui numeri naturali (oltre a quella di prendere il successivo \(\mathfrak{S}\), già definita in precedenza), che poi si estenderanno alle altre tipologie di numeri. In particolare ci concentriamo sulle operazioni aritmetiche fondamentali di somma \(+\), sottrazione \(-\), moltiplicazione \(*\) e divisione \(\div\).
Siano \(n,m\in \mathbb{N}\). La loro somma \(n+m\in \mathbb{N}\) è il numero ottenuto applicando a \(n\) l'operazione successivo \(m\) volte:
\begin{equation*} n+m= \mathfrak{S}^m(n)\; . \end{equation*}Risulta chiaro dalla definizione che \(n+m=m+n\). Si noti che è possibile anche definire la somma ricorsivamente, tramite le relazioni
\begin{align} &n+0 = n\; ,\\ &n+\mathfrak{S}(m)= \mathfrak{S}(n+m)\; . \end{align}La struttura ricorsiva dei numeri naturali, e la definizione di somma possono essere usati per confermare la validità dell'importante metodo dimostrativo per induzione.
Sia \(A(n)\) una frase in cui la variabile libera \(n\) è un numero naturale. Si supponga che: \(A(0)\) sia vera, e che valga l'inferenza \[ A(n)\longrightarrow A(n+1) \; .\] Allora \[ (\forall m\in \mathbb{N}) A(m)\; , \] ovvero \(A(m)\) è vera per ogni \(m\) numero naturale.
Per definizione di somma tra numeri naturali, \(n+1=\mathfrak{S}(n)\). Inoltre, per qualsiasi naturale \(m\), \(m=\mathfrak{S}^m(0)\) – si veda l'equazione \eqref{eq:0}.
Ora \(A(0)\) è vera, per cui, usando l'ipotesi induttiva \(A(n)\longrightarrow A(n+1)\) anche \(A(\mathfrak{S}(0))\) è vera. Utilizzando ripetutamente per altre \(m-1\) volte l'ipotesi induttiva si ha che anche \(A(\mathfrak{S}^{m}(0))=A(m)\) è vera. Dato che il numero naturale \(m\) è stato scelto in maniera arbitraria, la dimostrazione è conclusa.
Il principio di induzione sfrutta la ricorsività per evitare una verifica diretta che sarebbe impossibile. Basta infatti verificare due affermazioni per dimostrare che ne sono vere un numero infinito!
Siano \(n,m\in \mathbb{N}\), con \(m\leq n\). Allora la loro differenza \(n-m\in \mathbb{N}\) è il numero tale che agendo su di esso con \(\mathfrak{S}\) per \(m\) volte otteniamo \(n\), ovvero è l'unico numero naturale che soddisfa la relazione
\begin{equation*} n=\mathfrak{S}^m(n-m)= (n-m) + m\; . \end{equation*}L'operazione di sottrazione non si può applicare a tutte le coppie di numeri naturali ottenendo ancora un numero naturale, infatti possiamo applicarla solamente nel caso in cui il numero sottratto sia più piccolo o uguale a quello di partenza. Si dice quindi che i numeri naturali non sono chiusi rispetto all'operazione di sottrazione. Essi sono invece chiusi rispetto all'operazione di addizione, in quanto la somma di qualsiasi coppia di numeri naturali è ancora un numero naturale.
Siano \(n,m\in \mathbb{N}\). Allora il loro prodotto \(n* m\in \mathbb{N}\) è definito da
\begin{equation*} \label{eq:4} n* m = \underbrace{n+\dotsm +n}_{m}\; . \end{equation*}Risulta chiaro dalla definizione che \(n* m=m* n\). Si noti che anche il prodotto si può definire ricorsivamente, tramite le relazioni
\begin{align} &n * 0 = 0\; ,\\ &n*\mathfrak{S}(m)= n* m + n\; . \end{align}I numeri naturali sono chiusi rispetto al prodotto. Somma e prodotto seguono la ben nota regola di distribuzione seguente:
\begin{equation} \label{eq:5} (n+m)* \ell= (n* \ell) + (m* \ell)\; . \end{equation}L'operazione di divisione merita un discorso a parte. Essa infatti in generale non produce, nei numeri naturali, un altro numero naturale bensì una coppia di numeri naturali: il quoziente \(q\) ed il resto \(r\). Ciò è legato al fatto che i naturali non sono chiusi rispetto all'operazione di divisione; i numeri razionali saranno introdotti proprio allo scopo di definire il quoziente di numeri naturali come un numero anch'esso.
Siano \(n,m\in \mathbb{N}\), con \(m\neq 0\). Allora la divisione \(n\div m= (q,r)\in \mathbb{N}\times \mathbb{N}\) è una coppia di numeri, detti rispettivamente quoziente e resto, tali per cui \(r < m\) e
\begin{equation*} \label{eq:6} n= q*m+r\; . \end{equation*}Sia \(n\in \mathbb{N}\), \(n > 1\). Allora \(n\) si dice primo se e solo se \[ n\div m =(q,0) \; \longrightarrow\; m=1 \, \vee \, m=n\; .\]
Il teorema che segue, originariamente dovuto ad Euclide, è di fondamentale importanza. Esso ci dice come decomporre ogni numero naturale come prodotto di fattori primi.
Sia \(n\in \mathbb{N}\), \(n>1\). Allora o \(n\) è primo, o può essere scritto (in maniera unica) come prodotto di numeri primi.
Il numero \(50\) non è primo, ma può essere fattorizzato solamente nel modo seguente: \[50= 2 * 5 * 5 = 2 * 5^2\; .\]
3.2 Numeri Interi
I numeri interi sono l'estensione dei numeri naturali chiusa rispetto alla sottrazione, oltre che all'addizione e alla moltiplicazione. Si possono definire in varie maniere, qui si seguirà quella ora comunemente accettata in matematica.
Preliminarmente, discutiamo il concetto di relazione di equivalenza. Sia \(n\in \mathbb{N}\), e chiamiamo \(r_5(n)\in \{0,1,2,3,4\}\) il corrispondente resto di \(n\div 5\). Chiaramente \(r_5(0)=0\), \(r_5(1)=1\), … , \(r_5(4)= 4\); poi si ha che \(r_5(5)= 0\), \(r_5(6)= 1\), e così via. Quindi in particolare abbiamo che
\begin{equation} \label{eq:9} r_5(0)=r_5(5)=r_5(10)= \dotsc\; . \end{equation}Diciamo quindi che \(0,5,10\) sono equivalenti modulo 5. Più precisamente diciamo che due numeri \(n,m\in \mathbb{N}\) sono equivalenti modulo 5 – scritto \(n\sim_5 m\) – se e solo se \(r_5(n)=r_5(m)\). La relazione \(\sim_5\) è un esempio di relazione di equivalenza, solitamente denotata con il simbolo \(\sim\). Le relazioni di equivalenza ci permettono di raggruppare gli elementi di un dato insieme, in questo caso \(\mathbb{N}\): infatti possiamo definire la classe di equivalenza di un dato numero \(n\in \mathbb{N}\) come l'insieme (stiamo considerando nello specifico la relazione \(\sim_5\), ma la definizione è analoga per ciascuna relazione di equivalenza, per cui omettiamo il pedice \(_5\))
\begin{equation} \label{eq:10} [n]_{\sim}= \{m\in \mathbb{N}\,,\, m\sim n\}\; . \end{equation}Chiaramente \([n]_{\sim}\subseteq \mathbb{N}\), e \(\mathbb{N}\) si può suddividere nei sottoinsiemi rappresentati da tutte le classi di equivalenza distinte. Infatti dati due numeri \(n,m\), è possibile che \([n]_{\sim}=[m]_{\sim}\): è infatti necessario e sufficiente che \(n\sim m\).
Quante e quali sono le classi di equivalenza di \(\toggle{\texttip{\sim_5?}{Cliccando qui è possibile visualizzare la soluzione}}{\sim_5?\quad\textcolor{Red}{\text{Soluzione. Le classi sono 5: } [0]_{\sim_5}, [1]_{\sim_5}, [2]_{\sim_5}, [3]_{\sim_5}, [4]_{\sim_5}.}}\endtoggle\)
Chiameremo insieme quoziente, in questo caso \(\mathbb{N}/\!\!\sim\), l'insieme di tutte le classi di equivalenza. Ogni classe di equivalenza si può identificare con un qualsiasi dei suoi costituenti, che chiamiamo rappresentante, e ciò è implicito nella scrittura \([n]_{\sim}\): per definire univociamente la classe di equivalenza è sufficiente esplicitare \(n\). Per cui di fatto l'insieme \(\mathbb{N}/\!\!\sim\) si può pensare come un insieme di numeri (anche se in realtà è un insieme di insiemi), ove ciascun numero è un rappresentante della classe di equivalenza. Nel caso di \(\sim_5\), \(\mathbb{N}/\!\!\sim_5\) può di fatto essere identificato con l'insieme \(\toggle{\{?\}.}{\{0,1,2,3,4\}.}\endtoggle\)
Per definire i numeri interi, dobbiamo fare ricorso a una speciale classe di equivalenza fra coppie ordinate di numeri naturali \((P,N)\). Intuitivamente, il primo numero della coppia \(P\) rappresenta la parte positiva del numero intero, il secondo numero \(N\) la sua parte negativa. L'idea è che il numero intero \(2\) può essere visto come la coppia \((2,0)\), ma anche come la coppia \((3,1)\) o \((4,2)\), per cui vogliamo che tutte queste coppie siano equivalenti; identificheremo poi la loro classe di equivalenza con l'agognato numero (intero) \(2\).
Consideriamo quindi le coppie \((P,N)\in \mathbb{N}\times \mathbb{N}\), e definiamo la relazione di equivalenza \(\sim_{\mathbb{Z}}\) come
\begin{equation} \label{eq:11} (P,N)\sim_{\mathbb{Z}} (Q,M) \; \longleftrightarrow \; P+M=Q+N\; . \end{equation}Perché abbiamo formulato l'equivalenza in questo modo? Intuitivamente vorremmo dire che \(P-N=Q-M\), ma non possiamo farlo per coppie di numeri naturali arbitrari \((P,N)\) e \(Q,M\)! Infatti, per definire la sottrazione tra numeri naturali necessitiamo che \(P\geq N\) e \(Q\geq M\), ma ciò non ci permetterebbe di definire i negativi, che è proprio il nostro scopo. La relazione formulata in termini di somme come fatto in \eqref{eq:11} è però perfettamente lecita per qualsiasi coppia di naturali, ed è quindi la scelta giusta nel rispetto della nostra intuizione.
Definiamo l'insieme \(\mathbb{Z}\) dei numeri interi come l'insieme
\begin{equation*} \label{eq:12} \mathbb{Z} = (\mathbb{N}\times \mathbb{N})/ \!\!\sim_{\mathbb{Z}}\; . \end{equation*}Perché questa definizione sia ben posta, dobbiamo fare le seguenti cose:
- Identificare i numeri naturali (o interi non-negativi) all'interno dell'insieme dei numeri interi;
- Identificare i numeri negativi all'interno dell'insieme dei numeri interi;
- Definire le operazioni di somma, differenza, e moltiplicazione tra interi, e verificare che coincidano sui numeri naturali con le definizioni date nella §3.1.1;
- Definire le relazioni d'ordine \(<\) e \(\leq\) sugli interi, e verificare che coincidano sui numeri naturali con le definizioni date nella §3.1.
Come vedremo queste cose si possono fare in molto maniera intuitiva a partire dalla definizione di \(\sim_{\mathbb{Z}}\). Partiamo dai primi due punti, ovvero identificare i numeri naturali e i numeri negativi all'interno di \(\mathbb{Z}\).
Verificare che ciascuna classe di equivalenza \([(P,Q)]_{\sim_{\mathbb{Z}}}\) ha come rappresentante o \((n,0)\) oppure \((0,n)\), per un certo \(n\in \mathbb{N}\).
Identifichiamo \([(n,0)]_{\sim_{\mathbb{Z}}}\) con il numero naturale \(n\) (visto come numero intero) – scriveremo direttamente \(n\in \mathbb{Z}\) – e \([(0,n)]\), quando \(n>0\), con il numero intero negativo \(-n\) – scriveremo direttamente \(-n\in \mathbb{Z}\).
Passiamo ora alla definizione delle operazioni \(+,-,*\) tra numeri interi. Come vedremo è conveniente definire tali operazioni sulle coppie di interi \((P,N)\). Bisogna però prestare attenzione al fatto che le definizioni siano ben poste per le classi di equivalenza, ovvero che operando su rappresentativi diversi il risultato ottenuto appartenga sempre alla stessa classe di equivalenza. Invitiamo il lettore a verificare che ciò sia vero.
Siano \([(P,N)]_{\sim_{\mathbb{Z}}},[(Q,M)]_{\sim_{\mathbb{Z}}}\in \mathbb{Z}\). Allora definiamo la loro somma come l'intero
\begin{equation*} \label{eq:13} [(P,N)]_{\sim_{\mathbb{Z}}}+[(Q,M)]_{\sim_{\mathbb{Z}}}= [(P+Q,N+M)]_{\sim_{\mathbb{Z}}}\; . \end{equation*}In altre parole, la somma di due numeri interi è data dall'intero in cui si sono sommate, separatamente, le parti positive e negative.
Per due numeri naturali \(n,m\), che corrispondono alle classi di equivalenza delle coppie \((n,0)\) e \((m,0)\), otteniamo chiaramente lo stesso risultato che avremmo utilizzando la Definizione 3.1.1.1.
Siano \([(P,N)]_{\sim_{\mathbb{Z}}},[(Q,M)]_{\sim_{\mathbb{Z}}}\in \mathbb{Z}\). Allora definiamo il loro prodotto come l'intero
\begin{equation*} \label{eq:13a} [(P,N)]_{\sim_{\mathbb{Z}}} * [(Q,M)]_{\sim_{\mathbb{Z}}}= [(P * Q + N * M , P * M + N * Q)]_{\sim_{\mathbb{Z}}}\; . \end{equation*}Anche in questo caso per due numeri naturali \((n,0)\) e \(m,0\) abbiamo come prodotto \((n * m,0)\), in accordo con la Definizione 3.1.1.3.
Definiamo ora l'inverso additivo di un numero intero: basterà invertire la parte positiva e negativa
\begin{equation} \label{eq:14} -[(P,N)]_{\sim_{\mathbb{Z}}}= [(N,P)]_{\sim_{\mathbb{Z}}}\; . \end{equation}Grazie all'inverso additivo la definizione di sottrazione segue immediatamente.
Siano \([(P,N)]_{\sim_{\mathbb{Z}}},[(Q,M)]_{\sim_{\mathbb{Z}}}\in \mathbb{Z}\). Allora definiamo la loro differenza come l'intero
\begin{equation*} \label{eq:13b} [(P,N)]_{\sim_{\mathbb{Z}}} - [(Q,M)]_{\sim_{\mathbb{Z}}}= [(P,N)]_{\sim_{\mathbb{Z}}}+ \bigl(-[(Q,M)]_{\sim_{\mathbb{Z}}}\bigr)= [(P+M,N+Q)]_{\sim_{\mathbb{Z}}}\; . \end{equation*}Ancora una volta la differenza fra interi coincide sui naturali con quella definita in Definizione 3.1.1.2, col vantaggio che possiamo definirla per ciascuna coppia di interi. Segue quindi che gli interi sono chiusi rispetto alla sottrazione.
Rimane da definire la relazione d'ordine \( < \) fra interi (quella dell'ordine totale \(\leq \) segue immediatamente).
Siano \([(P,N)]_{\sim_{\mathbb{Z}}},[(Q,M)]_{\sim_{\mathbb{Z}}}\in \mathbb{Z}\). Allora
\begin{equation*} \label{eq:1} [(P,N)]_{\sim_{\mathbb{Z}}} < [(Q,M)]_{\sim_{\mathbb{Z}}} \; \longleftrightarrow \; P+M < N+Q\; . \end{equation*}Anche in questo caso la relazione d'ordine fra interi rispetta quella fra naturali. Ne consegue dunque che i numeri interi possono essere rappresentati graficamente in maniera analoga ai numeri naturali come sequenza totalmente ordinata di punti equidistanti; però tale sequenza si estende all'infinito da ambo i lati partendo dallo zero, verso destra con i numeri interi positivi \(n\in \mathbb{Z}\), (con \(0 < n\)), e verso sinistra con i numeri interi negativi \(-n\in \mathbb{Z}\) (sempre con \(0 < n\)). La relazione d'ordine, come per i numeri naturali, si percorre da sinistra verso destra, ovvero dati due numeri interi quello più a sinistra nella rappresentazione grafica è minore dell'altro.
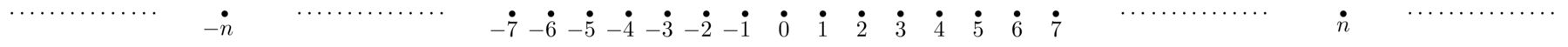
Figura 2: Rappresentazione grafica di \(\mathbb{Z}\)
Così come \(\mathbb{N}\) ha un mumero infinito di elementi, analogamente \(\mathbb{Z}\) ha un numero infinito di elementi. Non entreremo nei dettagli, ma la tipologia di infinito (detta cardinalità) dei due insiemi è la stessa, ovvero essi hanno lo "stesso numero infinito di elementi", detto cardinale numerabile \(\aleph_0\). L'appellativo di numerabile è dato per il fatto che questa tipologia di infinito si può contare (anche se per contarli tutti servirebbe un tempo infinito). Come vedremo alcuni insiemi di numeri sono talmente grandi da renderne impossibile il conteggio.
3.3 Numeri Razionali
I numeri razionali sono, a livello intuitivo, quelli che rappresentano frazioni – ovvero divisioni – di numeri interi. Rileggendo la Definizione 3.1.1.4 di divisione per numeri naturali (per i numeri interi sarebbe analoga, mutatis mutandis), risulta chiaro che anche i razionali dovranno essere costruiti a partire da coppie di numeri. E sarà nuovamente necessario identificare alcune delle coppie tra loro come equivalenti, definendo quindi opportune relazioni e classi di equivalenza. L'idea di base della costruzione è la seguente: la coppia di numeri definisce numeratore e denominatore del numero razionale. Per questo motivo, il secondo intero della coppia non potrà assumere il valore zero.
Prendiamo allora le coppie ordinate di interi rappresentanti numeratore e denominatore \((N,D)\in \mathbb{Z} \times (\mathbb{Z}\smallsetminus \{0\})\), dove nel secondo insieme di interi (il denominatore) abbiamo tolto lo zero. La relazione di equivalenza \(\sim_{\mathbb{Q}}\) si definisce in questo modo:
\begin{equation} \label{eq:2} (N,D)\sim_{\mathbb{Q}} (M,E) \; \longleftrightarrow \; N * E = M * D\; . \end{equation}Come per la definizione di interi la relazione di equivalenza "naturale" (ma non ammessa) sarebbe \(\frac{N}{D}= \frac{M}{E}\), che però può essere formulata legittimamente come appare in \eqref{eq:2}. I razionali non sono altro che le classi di equivalenza di \(\sim_{\mathbb{Q}}\) in \(\mathbb{Z}\times (\mathbb{Z}\smallsetminus \{0\})\).
Definiamo l'insieme \(\mathbb{Q}\) dei numeri razionali come l'insieme \[ \mathbb{Q} = \bigl(\mathbb{Z}\times (\mathbb{Z}\smallsetminus \{0\})\bigr)/\!\! \sim_{\mathbb{Q}} \; .\]
Per la definizione delle operazioni e della relazione d'ordine (totale) sui razionali si procede come abbiamo fatto per gli interi, questa volta identificando gli interi come sottoinsieme dei razionali, e verificando la consistenza delle operazioni razionali con quelle intere. Ci limitiamo dunque a presentare le definizioni in maniera veloce, invitando il lettore interessato a compendiare i dettagli, sulla falsa riga della sezione precedente.
\begin{align} \label{eq:15} &[(N,D)]_{\sim_{\mathbb{Q}}}+[(M,E)]_{\sim_{\mathbb{Q}}}= [(N * E + D * M,D * E)]_{\sim_{\mathbb{Q}}}\; ;\\ \label{eq:16} &[(N,D)]_{\sim_{\mathbb{Q}}}-[(M,E)]_{\sim_{\mathbb{Q}}}= [(N * E - D * M,D * E)]_{\sim_{\mathbb{Q}}}\; ;\\ \label{eq:17} &[(N,D)]_{\sim_{\mathbb{Q}}} * [(M,E)]_{\sim_{\mathbb{Q}}}= [(N * M, D * E)]_{\sim_{\mathbb{Q}}}\; ;\\ \label{eq:18} &[(N,D)]_{\sim_{\mathbb{Q}}} \div [(M,E)]_{\sim_{\mathbb{Q}}}= [(N * E, D * M)]_{\sim_{\mathbb{Q}}}\; ;\\ \label{eq:19} &[(N,D)]_{\sim_{\mathbb{Q}}} \leq [(M,E)]_{\sim_{\mathbb{Q}}} \longleftrightarrow\begin{cases} &N * E \leq D * M& \text{if } D * E > 0\\ &N * E \geq D * M& \text{if } D * E < 0 \end{cases}\; . \end{align}Utilizzando la notazione ben nota per i numeri razionali \(\frac{N}{D}\) (e omettendo il simbolo \( * \) di prodotto se ciò non causa confusione), le operazioni qui sopra si possono riscrivere nella maniera nota
\begin{align} & \frac{N}{D}+\frac{M}{E}= \frac{NE +MD}{DE}\; ,\\ & \frac{N}{D}-\frac{M}{E}= \frac{NE -MD}{DE}\; ,\\ & \frac{N}{D} * \frac{M}{E}= \frac{NM}{DE}\; ,\\ & \frac{N}{D} \div \frac{M}{E}= \frac{NE}{DM}\; . \end{align}I numeri razionali sono, in apparenza, tanti. Infatti, il seguente risultato è vero.
Siano \(p,q\in \mathbb{Q}\), con \(p < q\)1. Allora esiste \(r\in \mathbb{Q}\) tale che \[ p < r < q \; . \]
Quindi prendendo due numeri razionali distinti qualsivoglia, ne possiamo sempre trovare un altro, e quindi infiniti altri fra essi!
Si dimostri il Teorema 3.3.2. \(\toggle{\diamond}{\textcolor{Red}{\text{Suggerimento: si consideri } p=\frac{N}{D}\,,\, q=\frac{M}{E} \text{ con \(D,E > 0\), e } r=\frac{N+M}{D+E}}}\endtoggle\)
I numeri razionali, nonostante il Teorema 3.3.2 non sono però un'infinità più grande dei naturali, e sono anch'essi numerabili (e quindi di cardinalità \(\aleph_0\)). Non daremo una dimostrazione di questo fatto, che però può essere facilmente illustrato graficamente (ogni freccia corrisponde ad un aumento di uno nel conteggio).
Grazie ai numeri razionali abbiamo quindi "popolato" in maniera molto fitta la nostra rappresentazione grafica dei numeri, infatti tra ciascuna coppia di numeri interi dobbiamo inserire un'infinità di numeri razionali, e tra ciascuna coppia dei numeri razionali suddetti ce ne saranno a loro volta un'infinità di altri! Possiamo allora chiederci, è la rappresentazione grafica di \(\mathbb{Q}\) una retta ordinata, ovvero una successione continua (e ordinata2) di numeri?
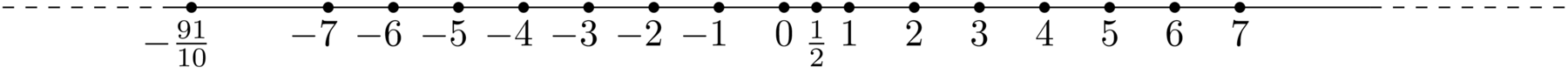
Figura 3: Rappresentazione grafica di \(\toggle{\mathbb{Q}?}{\mathbb{Q} \; \underline{\text{erronea}}}\endtoggle\)
La risposta è no, i numeri razionali non sono un continuo! Il perché lo spiegheremo nella prossima sezione, introducendo il concetto di taglio di Dedekind e di numero reale.
3.4 Numeri Reali
3.4.1 Tagli di Dedekind
Per verificare che i razionali non sono un continuo di numeri, introduciamo il concetto di taglio introdotto da Joseph Bertrand e poi ripreso da Richard Dedekind e da cui oggi prende il nome.
L'idea è la seguente. Vogliamo suddividere (tagliare) l'insieme \(\mathbb{Q}\) in due parti, chiamiamole \(A\) e \(B\), che rispettino le seguenti proprietà:
- \(A\neq \varnothing \) e \(A\neq \mathbb{Q}\);
- Se \(p,q\in \mathbb{Q}\), \(p < q\), e \(q\in A\), allora \(p\in A\). (\(A\) è "chiuso all'ingiù");
- Se \(p\in A\), allora esiste \(q\in A\) tale che \(q > p\). (\(A\) non contiene un massimo3);
- \(B=\mathbb{Q}\smallsetminus A\).
Siano \(A,B\subset \mathbb{Q}\) che soddisfino le proprietà qui sopra. Chiamiamo taglio di Dedekind \((A\vert B)\) di \(\mathbb{Q}\) la coppia ordinata \((A,B)\).
Come si può dedurre dalla definizione, per definire il taglio di Dedekind è sufficiente definire l'insieme \(A\), in quanto \(B\) non è nient'altro che il complementare \(A^{\mathrm{c}}\) di \(A\) in \(\mathbb{Q}\).
Nell'utilizzo dei tagli di Dedekind gioca un ruolo cruciale che l'insieme \(A\) non abbia un massimo. Ciò significa che, nel caso in cui i razionali fossero un continuo, allora \(B\) dovrebbe sempre avere un elemento minimo. Infatti, se anche \(B\) non ha un elemento minimo, allora significa che i razionali hanno un "buco" in corrispondenza del taglio, e non possono quindi essere un continuo.
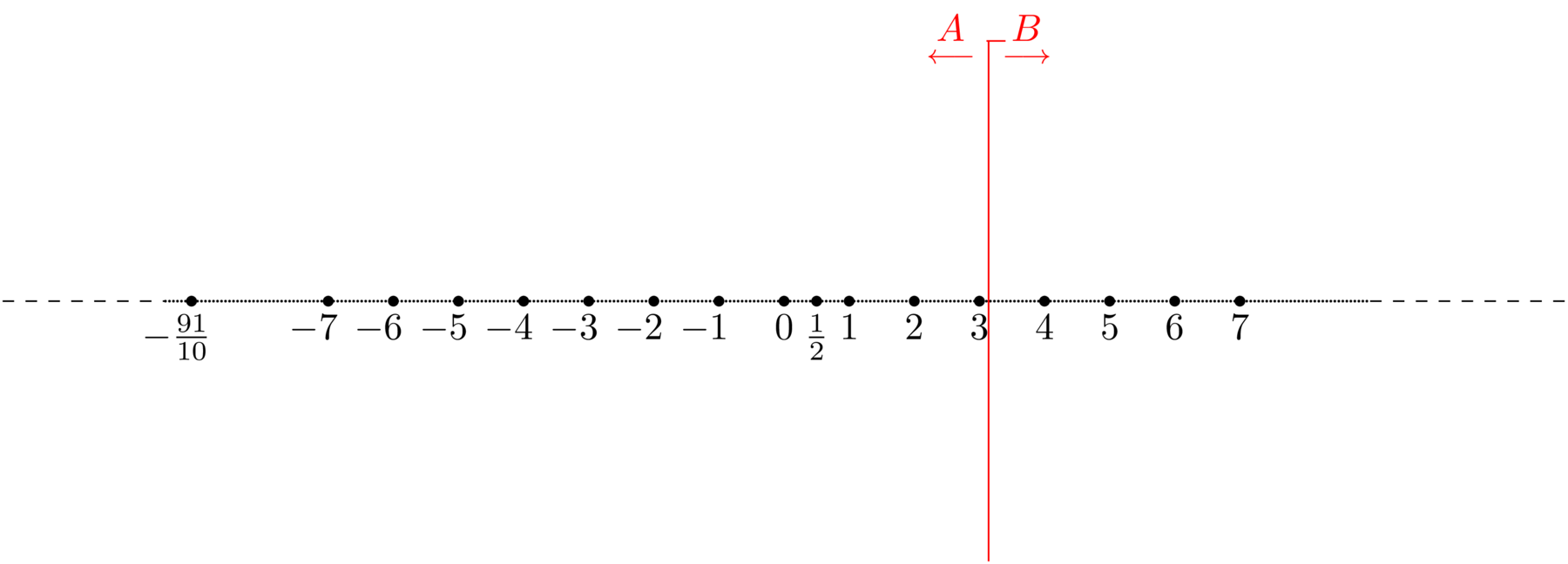
Figura 4: Rappresentazione grafica di un taglio di Dedekind di \(\mathbb{Q}\) (in rosso).
Definiamo alcuni tagli di Dedekind espliciti, e cerchiamo di capire se taglino i razionali in corrispondenza di un razionale, o meno. Per ragioni che saranno chiare a breve, assegniamo già un nome conveniente a tali tagli. Sia \(q\in \mathbb{Q}\) un numero razionale, allora definiamo4
\begin{align} \label{eq:3} q&=\bigl(\;\{p\in \mathbb{Q}\;,\; p < q\}\; \big\vert \; \{p\in \mathbb{Q}\;,\; p\geq q\}\;\bigr)\;;\\ \label{eq:sq2} \sqrt{2}&= \bigl(\; \{p\in \mathbb{Q}\;,\; p^2 < 2 \, \vee\, p < 0\}\; \big\vert \; \{p\in \mathbb{Q}\;,\; p^2\geq 2\, \land \, p > 0\}\; \bigr)\;;\\ \notag A_e&=\bigl\{p\in \mathbb{Q}\;,\; \exists n\in \mathbb{N} \bigl(p < 1+\tfrac{1}{1!}+\tfrac{1}{2!}+\dotsm+ \tfrac{1}{n!}\bigr)\bigr\}\; ,\\ \label{eq:e} e&= ( A_e\vert A_e^{\rm c})\;;\\ \notag A_{\pi}&=\bigl\{p\in \mathbb{Q}\,,\, \exists n\!\in\! \mathbb{N} \bigl(p < 4-\tfrac{4}{3} +\tfrac{4}{5}-\tfrac{4}{7}+ \dotsm+ \tfrac{4}{4n+1}-\tfrac{4}{4n+3}\bigr)\bigr\}\;,\\ \label{eq:pi} \pi&= ( A_\pi\vert A_\pi^{\rm c})\;. \end{align}Verificare che i tagli definiti dalle equazioni \eqref{eq:3}-\eqref{eq:pi} siano tagli di Dedekind.
Scrivere esplicitamente gli insiemi \[\toggle{A_e^{\rm c}=\bigl\{p\in \mathbb{Q}\;,\; \exists n\in \mathbb{N} \bigl(p < 1+\tfrac{1}{1!}+\tfrac{1}{2!}+\dotsm+ \tfrac{1}{n!}\bigr)\bigr\}^{\rm c}}{\textcolor{Red}{\text{Soluzione: } A_e^{\rm c}=\bigl\{p\in \mathbb{Q}\;,\; \exists n\in \mathbb{N} \bigl(p < 1+\tfrac{1}{1!}+\tfrac{1}{2!}+\dotsm+ \tfrac{1}{n!}\bigr)\bigr\}^{\rm c}= \bigl\{p\in \mathbb{Q}\;,\; \forall n\in \mathbb{N} \bigl(p \geq 1+\tfrac{1}{1!}+\tfrac{1}{2!}+\dotsm+ \tfrac{1}{n!}\bigr)\bigr\}}}\endtoggle\] e \[\toggle{A_{\pi}^{\rm c}=\bigl\{p\in \mathbb{Q}\;,\; \exists n\in \mathbb{N} \bigl(p < 4-\tfrac{4}{3} + \dotsm+ \tfrac{4}{4n+1}-\tfrac{4}{4n+3}\bigr)\bigr\}^{\rm c}}{\textcolor{Red}{\text{Soluzione: } A_{\pi}^{\rm c}=\bigl\{p\in \mathbb{Q}\;,\; \exists n\in \mathbb{N} \bigl(p < 4-\tfrac{4}{3} + \dotsm+ \tfrac{4}{4n+1}-\tfrac{4}{4n+3}\bigr)\bigr\}^{\rm c}= \bigl\{p\in \mathbb{Q}\;,\; \forall n\in \mathbb{N} \bigl(p \geq 4-\tfrac{4}{3} + \dotsm+ \tfrac{4}{4n+1}-\tfrac{4}{4n+3}\bigr)\bigr\}}}\endtoggle\; .\]
Il taglio di Dedekind definito dall'equazione \eqref{eq:3} avviene in corrispondenza del numero razionale \(q\). Infatti il secondo insieme del taglio \(\{p\in \mathbb{Q}\;,\; p\geq q\}\) ha un elemento minimo, dato proprio da \(q\), dato che i razionali sono totalmente ordinati. Quindi possiamo identificare i tagli di Dedekind \eqref{eq:3} con ciascun numero razionale \(q\in \mathbb{Q}\). I tagli di Dedekind possibili però sono molti di più dei numeri razionali; in particolare riempiono tutti i "buchi" nel continuo lasciati dai razionali: incominciamo col notare che i tagli \(\sqrt{2},e,\pi\) definiti rispettivamente dalle equazioni \eqref{eq:sq2}, \eqref{eq:e} e \eqref{eq:pi} non avvengono in corrispondenza di alcun numero razionale. Per fare ciò, bisogna dimostrare che il secondo insieme di ciascuno di tali tagli non ha un elemento minimo nei razionali. Forniremo una dimostrazione solo nel caso di \(\sqrt{2}\), ma dimostrazioni analoghe sono possibili anche per \(e\) e \(\pi\).
L'insieme \[\bigl\{p\in \mathbb{Q}\;,\; p^2\geq 2\, \land \, p > 0\bigr\}\] non ha un minimo, ovvero \(\sqrt{2}\notin \mathbb{Q}\).
Supponiamo che esista un numero razionale \(\underline{q}\in \mathbb{Q}\) tale che \(\underline{q}^2=2\). Se esistesse, esso sarebbe per definizione il minimo dell'insieme \[\{p\in \mathbb{Q}\;,\; p^2\geq 2\, \land \, p > 0\}\; .\] Ma se \(\underline{q}\) è razionale, allora esistono \(N,D\in \mathbb{N}\smallsetminus \{0\}\), con \(N,D\) coprimi5 tali che \(\underline{q}=\frac{N}{D}\). Per cui, \[ N^2= 2D^2\; .\] Ora sia \(N^2\) che \(2D^2\) sono numeri naturali, per cui per il Teorema 3.1.7 hanno una fattorizzazione unica in fattori primi. Inoltre, dato che \(N^2= 2D^2\) le due fattorizzazioni devono coincidere. Ma la fattorizzazione di sinistra avrà un numero zero o pari di fattori \(2\), mentre quella a destra un numero dispari di fattori \(2\). Ciò è in contraddizione con l'ipotesi che le due fattorizzazioni siano uguali, per cui \(\underline{q}\) non può essere un numero razionale.
Ciò dimostra che esistono dei buchi nei numeri razionali, in corrispondenza di opportuni tagli di Dedekind. Tali tagli definiscono dei numeri, detti numeri irrazionali. Anche i numeri razionali possono essere visti come tagli di Dedekind, per cui collezioniamo tutti i possibili tagli di Dedekind in un nuovo insieme numerico, che chiameremo l'insieme dei numeri reali.
Definiamo l'insieme \(\mathbb{R}\) dei numeri reali come l'insieme: \[ \mathbb{R}=\{ r\;,\; r=(A\vert B) \text{ taglio di Dedekind di } \mathbb{Q}\}\; .\]
Come abbiamo visto l'insieme dei numeri reali è costituito dai numeri razionali \(q\in \mathbb{Q}\) – visti come tagli di Dedekind \eqref{eq:3} – i cui "buchi sono riempiti" dai numeri irrazionali, definiti da tagli come \(\sqrt{2}\), \(\pi\) o \(e\) fino a formare un continuo di numeri. Infatti se costruissimo dei tagli di Dedekind di \(\mathbb{R}\) invece che di \(\mathbb{Q}\), avremmo che l'insieme \(B\) ha sempre un minimo reale (l'insieme dei tagli di Dedekind di \(\mathbb{R}\) coinciderebbe ancora con \(\mathbb{R}\) stesso).
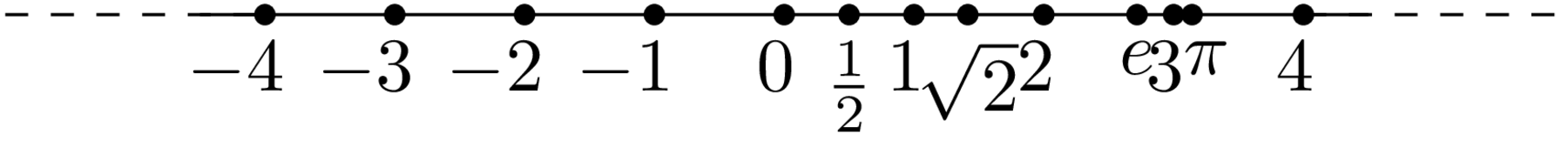
Figura 5: Rappresentazione grafica di \(\mathbb{R}\) come retta numerica.
I numeri irrazionali sono tanti. Infatti, l'ordine di infinito di \(\mathbb{R}\) è non numerabile! La sua cardinalità, detta cardinalità del continuo, si denota con \(2^{\aleph_0}\), e si ha che \(2^{\aleph_0} > \aleph_0\) (come numeri cardinali). Il fatto che i numeri reali non siano numerabili fa si che non sia possibile scrivere in maniera conveniente i numeri reali, ovvero tramite un numero finito di simboli (cosa invece possibile per i numeri naturali, interi, e razionali che possono essere scritti usando un numero finito di simboli appartenenti all'insieme \(\{0,1,2,3,4,5,6,7,8,9, /, -\}\), dove il penultimo simbolo rappresenta la frazione e l'ultimo il segno meno). Per ogni numero irrazionale si dovrebbe quindi scegliere un simbolo ad hoc che lo rappresenti! Se ciò viene comunemente fatto per alcuni numeri irrazionali particolarmente facili da definire o ricorrenti come ad esempio \(\sqrt[5]{3},\pi,e\) e \(\varphi\), non è chiaramente possibile farlo per tutti i numeri irrazionali, anche volendo dare fondo ad ogni possibile simbolo UniCode esistente (🔔,🗞,〠,💩, etc). Inoltre non tutti i numeri irrazionali hanno definizioni "semplici" come quelli sopra citati; il lettore interessato può leggere questa pagina per ulteriori dettagli.
3.4.2 Operazioni fra i numeri reali
Le operazioni e la relazione d'ordine totale definite su \(\mathbb{Q}\) si possono estendere ai tagli di Dedekind, e quindi ai numeri reali. Discutiamole brevemente. Dati due insiemi numerici \(S,T\subseteq \mathbb{Q}\), definiamo preliminarmente gli insiemi:
\begin{align} \label{eq:20} &S+T=\{s+t\;,\; s\in S\, \land \, t\in T\}\; ,\\ &S - T=\{s-t\; ,\; s\in S\, \land\, t\in T\}\; ,\\ &S * T=\{s * t\;, \; s\in S\, \land\, t\in T\}\;,\\ &S \div T=\{s \div t \; ,\; s\in S\, \land \, t\in T\}\; ,\\ &S_+=\{s\in S\;,\; s\geq 0\}\; . \end{align}Siano \(r_1,r_2\in \mathbb{R}\) corrispondenti rispettivamente a due tagli di Dedekind \((A_1\vert B_1), (A_2\vert B_2)\). Diciamo che \(r_1\leq r_2\) se e solo se \[ A_1\subseteq A_2 \; .\]
Siano \(r_1,r_2\in \mathbb{R}\) corrispondenti rispettivamente a due tagli di Dedekind \((A_1\vert B_1), (A_2\vert B_2)\). Allora la loro somma \(r_1+r_2\) è il taglio di Dedekind \[ r_1+r_2=\bigl( A_1+A_2 \big\vert(A_1+A_2)^{\rm c}\bigr) \; . \]
Siano \(r_1,r_2\in \mathbb{R}\) corrispondenti rispettivamente a due tagli di Dedekind \((A_1\vert B_1), (A_2\vert B_2)\). Allora la loro differenza \(r_1-r_2\) è il taglio di Dedekind \[ r_1-r_2=\bigl( A_1- (\mathbb{Q} \setminus A_2) \big\vert(A_1- (\mathbb{Q} \setminus A_2))^{\rm c}\bigr) \; . \]
Da ciò segue che il negativo del numero \(r\in \mathbb{R}\) corrispondente al taglio di Dedekind \((A\vert B)\) è dato da \[-r=\bigl( \mathbb{Q}_+^{\rm c}- (\mathbb{Q} \setminus A) \big\vert(\mathbb{Q}_+^{\rm c}- (\mathbb{Q} \setminus A))^{\rm c}\bigr) \; .\]
Siano \(r_1,r_2\in \mathbb{R}\) corrispondenti rispettivamente a due tagli di Dedekind \((A_1\vert B_1), (A_2\vert B_2)\). Allora il loro prodotto \(r_1 * r_2\) è il taglio di Dedekind seguente: se \(r_1,r_2\geq 0\), \[ r_1 * r_2=\Bigl( \bigl((A_1)_+ * (A_2)_+\bigr)\cup \mathbb{Q}_+^{\rm c} \Big\vert\bigl(\bigl((A_1)_+ * (A_2)_+\bigr)\cup \mathbb{Q}_+^{\rm c}\bigr)^{\rm c}\Bigr) \; . \]
Se almeno uno fra \(r_1\) e \(r_2\) è minore di zero, usiamo le seguenti relazioni per ricondurci alla definizione di prodotto di numeri reali positivi e a quella di negativo di un numero reale (si veda la Definizione 3.4.2.3): \[ r_1 * r_2 = -\bigl(r_1 * (-r_2)\bigr)= -\bigl((-r_1) * r_2\bigr)= \bigl((-r_1) * (-r_2)\bigr)\; .\]
Siano \(r_1,r_2\in \mathbb{R}\) corrispondenti rispettivamente a due tagli di Dedekind \((A_1\vert B_1), (A_2\vert B_2)\). Allora il loro quoziente \(r_1 \div r_2\) è il taglio di Dedekind seguente: se \(r_1\geq 0\) e \(r_2 > 0\), \[ r_1 \div r_2=\Bigl( A_1 \div (\mathbb{Q} \smallsetminus A_2) \Big\vert\bigl(A_1 \div (\mathbb{Q} \smallsetminus A_2)\bigr)^{\rm c}\Bigr) \; . \]
Se almeno uno fra \(r_1\) e \(r_2\) è minore di zero, usiamo le seguenti relazioni per ricondurci alla definizione di divisione di numeri reali positivi e a quella di negativo di un numero reale (si veda la Definizione 3.4.2.3): \[ r_1 \div r_2 = -\bigl(r_1 \div (-r_2)\bigr)= -\bigl((-r_1) \div r_2\bigr)= \bigl((-r_1) \div (-r_2)\bigr)\; .\]
4 Successioni
4.1 Le successioni come stringhe di numeri reali
Nella §2 abbiamo definito il concetto di coppia ordinata \((a,b)\). Estendiamo ora (informalmente) tale concetto per definire stringhe, o \(n\)-upla ordinate, di numeri. Siano \(a_0,a_1,a_2,\dotsc,a_n\) \(n\) numeri (ad esempio reali). Con essi possiamo convenientemente formare una \(n\)-upla ordinata, o stringa \[ A_{(n)}=(a_0,a_1,a_2,\dotsc,a_n) \] il cui ordine segue quello dei numeri naturali \(_0,_1,_2,\dotsc,_n\) che abbiamo usato come pedice (possiamo di fatto dire di aver scelto l'ordine della stringa proprio scegliendo di chiamare \(a_0\) il primo numero, \(a_1\) il secondo, etc). Possiamo anche pensare di considerare una stringa infinita (ma numerabile) di numeri reali, aumentando l'indice \(n\) fino all'infinito: \(A_{(\infty)}=(a_0,a_1,a_2,\dotsc,a_n,a_{n+1},\dotsc)\; .\)
È conveniente adottare le seguenti notazioni equivalenti per la stringa \(A_{(\infty)}\) (utilizzeremo prevalentemente la prima): \[A_{(\infty)} = (a_n)_{n\in \mathbb{N}}= (a_n)_{n=1}^{\infty} \; .\]
Inoltre d'ora in poi ci scorderemo della notazione \(A_{(\infty)}\), e chiameremo successione di numeri ogni stringa infinita di numeri.
Chiamiamo successione di numeri (naturali, interi, razionali, reali), denotata col simbolo \((a_n)_{n\in \mathbb{N}}\), una stringa infinita di numeri (naturali, interi, razionali, reali).
Sia \(r\in \mathbb{R}\smallsetminus \{0\}\) un numero reale diverso da zero. La progressione geometrica di ragione \(r\) è la successione \((a_n)_{n\in \mathbb{N}}\) tale che \[ a_n=r^n\; .\]
La sequenza di Fibonacci è la successione \((a_n)_{n\in \mathbb{N}}\) di numeri naturali tale per cui \(a_0=0\), \(a_1=1\), e per ogni \(n\geq 2\), \[ a_n=a_{n-1}+a_{n-2}\; . \]
La sequenza di Fibonacci ha quindi la forma esplicita \[ (0,1,1,2,3,5,8,13,21,34,55,89,\dotsc)\; .\]
4.2 Successioni convergenti
Un importante concetto legato alle successioni numeriche è quello di convergenza. Una successione numerica \((a_n)_{n\in \mathbb{N}}\) può essere vista graficamente come una sequenza di un numero infinito punti sulla retta numerica, disegnati ordinatamente uno dopo l'altro. In alcuni casi tali punti si avvicinano sempre più, al crescere dell'indice \(_n\) della successione, ad un certo valore \(a_{\infty}\) sulla retta numerica. In questo caso si dice che la successione converge, e si chiama \(a_{\infty}\) il suo valore limite.
Come possiamo definire matematicamente il concetto di "si avvicina sempre più"? Introduciamo il concetto di vicinato di un numero reale. Preliminarmente, definiamo intervallo (aperto o chiuso) sulla retta reale un suo segmento.
Si chiama intervallo aperto (limitato) di estremi \(a\in \mathbb{R}\) e \(b\in\mathbb{R}\) l'insieme numerico \[ ]a,b[ = \{r\in \mathbb{R}\;,\; a < r < b\}\; . \] Si chiama intervallo chiuso (limitato) di estremi \(a\in \mathbb{R}\) e \(b\in \mathbb{R}\) l'insieme \[ [a,b] = \{r\in \mathbb{R}\;,\; a\leq r \leq b\}\; .\]
La notazione è suggestiva del fatto che nell'intervallo aperto non si includono gli estremi del segmento individuato sulla retta numerica, mentre in quello chiuso si.
Sia \(a\in \mathbb{R}\). Si dice vicinato (simmetrico) di \(a\) qualsiasi intervallo aperto della forma \[ V_a(\varepsilon)= ] a-\varepsilon, a+\varepsilon[ \] per qualche \(\varepsilon \in \mathbb{R}\), \(\varepsilon > 0\).
Chiamiamo sistema fondamentale di vicinati di \(a\) la collezione di intervalli: \[ \mathscr{V}_a=\{ V_a(\varepsilon)\;,\; \varepsilon > 0\} \; . \]
Grazie al concetto di vicinato, possiamo ora chiarire come una successione si possa avvicinare sempre più ad un certo numero. Dato un vicinato \(V_a(\varepsilon)\), diciamo che la successione \((a_n)_{n\in \mathbb{N}}\) è eventualmente in \(V_a(\varepsilon)\) se esiste un numero naturale \(\underline{n}\in \mathbb{N}\) tale per cui \[ (\forall n\geq \underline{n})\; a_n\in V_a(\varepsilon)\; . \]
Sia \((a_n)_{n\in \mathbb{N}}\) una successione di numeri reali. Diciamo che \(( a_n)_{n\in \mathbb{N}}\) converge ad \(a_{\infty}\in \mathbb{R}\), denotato con \[ a_n\underset{n\to \infty}{\longrightarrow} a_{\infty}\;,\; \lim_{n\to \infty} a_n=a_{\infty}\; ,\] se e solo se \((a_n)_{n\in \mathbb{N}}\) è eventualmente in ogni \(V_{a_{\infty}}(\varepsilon)\in \mathscr{V}_{a_{\infty}}\).
Una successione è convergente se converge ad un qualsiasi valore \(a\in \mathbb{R}\). Una successione è detta non convergente se e solo se non converge a nessun \(a\in \mathbb{R}\).
Come possiamo quantificare la nozione di convergenza appena data? Utilizzando il concetto di valore assoluto. Dato un numero reale \(r\in \mathbb{R}\), definiamo il suo valore assoluto, o modulo nel seguente modo6: \[ \lvert r \rvert_{}^{}=\max\{r,-r\} \; . \]
Ora possiamo riformulare il concetto di convergenza nel modo seguente: \[ a_n\underset{n\to \infty}{\longrightarrow} a_{\infty} \; \longleftrightarrow \; (\forall\varepsilon > 0)(\exists \underline{n}\in \mathbb{N})(\forall n\geq \underline{n})\, \lvert a_n -a_{\infty} \rvert_{}^{} < \varepsilon \; . \]
Sia \((a_n)_{n\in \mathbb{N}}\) la successione con \[ a_n=\frac{1}{n+1}\; . \]
Esplicitamente, \[ \Bigl(1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\dotsc\Bigr)\; .\] Intuitivamente, tale successione è formata da numeri positivi via via più piccoli, e quindi potrebbe convergere a zero. Dimostriamo che è così.
Sia \(\varepsilon > 0\). Allora \[ \Bigl\lvert \frac{1}{n+1} \Bigr\rvert_{}^{}= \frac{1}{n+1} < \varepsilon \; \longleftrightarrow \; n > \frac{1-\varepsilon}{\varepsilon}\; .\] Quindi, se scegliamo7 \(\underline{n}= \Bigl\lceil\frac{1-\varepsilon}{\varepsilon}\Bigr\rceil\), abbiamo: \(\forall n\geq \Bigl\lceil\frac{1-\varepsilon}{\varepsilon}\Bigr\rceil\), \[ \Bigl\lvert \frac{1}{n+1} -0\Bigr\rvert_{}^{}= \Bigl\lvert \frac{1}{n+1} \Bigr\rvert_{}^{}<\varepsilon\; . \] Per cui \[ \lim_{n\to \infty} \frac{1}{n+1}=0 \; .\]
La progressione geometrica converge? La risposta è dipende.
Cominciamo con il considerare il caso in cui la ragione sia \(r=1\). Allora la progressione geometrica non progredisce molto: \[ (1,1,1,\dotsc,1,\dotsc) \; . \] In questo caso dovremmo essere in grado facilmente di dimostrare che \((1^n\underset{n\to \infty}{\longrightarrow} 1)\). In effetti si ha che per ogni \(\varepsilon > 0\) e \(n\in \mathbb{N}\), \[ \lvert 1^n - 1 \rvert_{}^{}=0 < \varepsilon \; . \] La condizione di convergenza è quindi soddisfatta banalmente con \(\underline{n}=0\) per ogni \(\varepsilon > 0\).
Consideriamo ora il caso in cui \(r > 1\). In questo caso la progressione geometrica cresce sempre; in particolare qualsiasi siano \(a,b \in \mathbb{R}\), esiste un \(n(a,b)\in \mathbb{N}\) tale che per ogni \(n\geq n(a,b)\), \[ r^n-a \geq b \; . \] Supponiamo che esista, fissato \(a\in \mathbb{R}\) ed un certo \(\varepsilon > 0\), \(\underline{n} \in \mathbb{N}\) tale che \[ \lvert r^{\underline{n}} -a \rvert_{}^{} < \varepsilon \; .\] Ma allora significa che \(\underline{n} < n(a,\varepsilon)\), e per ogni \(n\geq n(a,\varepsilon)\), \[ r^n-a = \lvert r^n - a \rvert \geq \varepsilon \; .\] Per cui la progressione geometrica diverge, per ogni ragione \(r > 1\).
Se \(0 < r < 1\), allora \(\texttip{r^{n+1} < r^n}{Perché?}\). Quindi al crescere di \(n\), il numero \(r^n\) decresce. Quindi l'intuizione ci dice che potrebbe convergere a \(0\). Dimostriamo che la nostra intuizione è giusta. Se \(\varepsilon \geq 1\), allora possiamo scegliere \(\underline{n}=0\): per ogni \(n\in \mathbb{N}\), \[ \lvert r^n - 0 \rvert_{}^{}=r^n < 1\leq \varepsilon\; . \] Se \(0 < \varepsilon < 1\), allora abbiamo che8 \[ r^n < \varepsilon \; \longleftrightarrow \; \log_r r^n > \log_r \varepsilon \; \longleftrightarrow \; n > \log_r \varepsilon \; .\] Da ciò segue che possiamo scegliere \(\underline{n}\) come il più piccolo numero naturale più grande o uguale a \(\log_r \varepsilon\), e ottenere per ogni \(n\geq \underline{n}\) \[ \lvert r^n -0 \rvert_{}^{}= r^n <\varepsilon\; . \] Ciò dimostra la convergenza di \(r^n\) a zero, quando \(0 < r <1\).
Discutere la convergenza della progressione geometrica per \(r < 0\).
Abbiamo quindi dimostrato il lemma seguente.
Sia \(\bigl(a_n(r)\bigr)_{n\in \mathbb{N}}\) la progressione geometrica di ragione \(r\neq 0\). Allora \(\bigl(a_n(r)\bigr)_{n\in \mathbb{N}}\) converge se e solo se \(\lvert r \rvert_{}^{} < 1\) o \(r=1\). In tal caso, \[ \lim_{n\to \infty} a_n(r)= \begin{cases} &0 &\text{se }\lvert r \rvert_{}^{}<1 \\ &1 & \text{se }r=1\\ \end{cases}\; . \]
Definiamo ora il comportamento di successioni di numeri che diventano o sempre più grandi, o sempre più piccoli.
Sia \((a_n)_{n\in \mathbb{N}}\) una successione di numeri reali. Diciamo che \((a_n)_{n\in \mathbb{N}}\) diverge a \(\pm \infty\), denotato con \[ a_n\underset{n\to \infty}{\longrightarrow} \pm \infty\;,\; \lim_{n\to \infty} a_n= \pm \infty\; ,\] se e solo se per ogni \(M > 0\), esiste \(\underline{n}\in \mathbb{N}\) tale che \(\forall n\geq \underline{n}\), \(a_n \gtrless 0\) e: \[\bigl\lvert a_n \bigr\rvert_{}^{} \geq M\; .\]
È banale, e quindi non lo dimostreremo, capire che se una successione diverge verso \(+\infty\) o \(-\infty\), allora non può allo stesso tempo convergere verso alcun numero reale.
Se una successione diverge a \(\pm\infty\), allora non può convergere verso nessun \(a\in \mathbb{R}\).
Sia \((a_n)_{n\in \mathbb{N}}\) la successione tale che \(a_n=n\), e \((b_n)_{n\in \mathbb{N}}\) quella tale che \(b_n=-n\). Allora \[ \lim_{n\to \infty}a_n=+\infty\; ,\; \lim_{n\to \infty} b_n=-\infty\; .\]
Dimostrare l'affermazione dell'esempio precedente. \(\toggle{\diamond}{\textcolor{Red}{\text{Suggerimento: Per ogni \(M > 0\), prendere \(\underline{n}= \lceil M \rceil\).}}}\endtoggle\)
Si tenga a mente che esistono successioni che diventano alternativamente sempre più grandi e sempre più piccole, e che quindi non convergono ma non divergono né a \(+\infty\), né a \(-\infty\), secondo la nostra definizione. Successioni che oscillano tra valori maggiori e minori di un determinato numero (solitamente zero) vengono anche chiamate successioni oscillanti. Tre esempi di successioni oscillanti \((a_n)_{n\in \mathbb{N}}\) sono dati da:
\begin{align*} a_n&=(-1)^n\; ,\\ a_n&=(-1)^n n\; ,\\ a_n&= \frac{(-1)^n}{n}\; . \end{align*}Le prime due non convergono (e nella seconda i valori con indice pari diventano sempre più grandi, mentre quelli con indice dispari sempre più piccoli), mentre la terza converge a zero.
4.2.1 Unicità del limite
Il limite di una successione, se esiste, è unico. Questo risultato, alla luce del Lemma 4.2.6 subito sotto alla Definizione 4.2.5, si estende anche a \(\pm\infty\) visti come "limiti" di successioni divergenti.
Sia \((a_n)_{n\in \mathbb{R}}\) una successione convergente verso \(a\in \mathbb{R}\), oppure divergente verso \(\pm\infty\). Allora il suo limite (rispettivamente \(a,\pm \infty\)) è unico.
Alla luce del già citato Lemma 4.2.6 sarà sufficiente dimostrare il teorema nel caso in cui la successione sia convergente verso \(a\in \mathbb{R}\).
Supponiamo che esista \(b\in \mathbb{R}\) tale che \[\lim_{n\to \infty}a_n=b\; .\] Allora, per ogni \(\varepsilon > 0\), abbiamo che9 \[ \lvert a-b \rvert_{}^{}= \lvert a- a_n + a_n - b \rvert_{}^{} \leq \lvert a- a_n \rvert_{}^{}+ \lvert a_n - b \rvert_{}^{}< 2\varepsilon\] a patto che \(n\geq \max\{\underline{n}(a), \underline{n}(b)\}\) (i due valori di \(\underline{n}\), a \(\varepsilon\) fissato, corrispondenti alle due convergenze verso \(a\) e \(b\) rispettivamente). Ovvero abbiamo che per ogni \(\varepsilon > 0\), \[\lvert a-b \rvert_{}^{}<2\varepsilon \; .\] Ciò è possibile solo se \(a=b\), infatti se \(a\neq b\) allora \(\lvert a-b \rvert_{}^{}>0\), e scegliendo allora \(3\varepsilon=\lvert a-b \rvert_{}^{}\) otterremmo \[ 3\varepsilon < 2\varepsilon \, \longleftrightarrow \, 3 < 2 \qquad {\Large ↯}\]
4.3 Combinazione di Limiti
I limiti di successioni possono essere combinati tramite operazioni aritmetiche, in maniera conveniente. Infatti l'idea è che, operativamente, sia sufficiente conoscere alcuni limiti "notevoli", da cui poi si possono ricavare altri apparentemente più complessi tramite semplici operazioni aritmetiche. Per poter operare sui limiti aritmeticamente, è bene chiarire il significato di alcuni simboli, apparentemente ambigui.
Innanzitutto, definiamo le seguenti uguaglianze: sia \(a\in \mathbb{R}\); \(\alpha > 1\); e \(0^{\pm}\) un numero molto vicino a zero, ma rispettivamente positivo o negativo; allora
\(\phantom{i}\)
- \[\pm \infty +a = \pm \infty\; ,\] \(\phantom{i}\)
- \[+\infty +\infty = +\infty\;,\] \(\phantom{i}\)
- \[-\infty -\infty = - \infty\; ,\] \(\phantom{i}\)
- \[\frac{1}{\pm\infty} = 0\; ,\] \(\phantom{i}\)
- \[\frac{1}{0^{\pm}}= \pm \infty \;,\] \(\phantom{i}\)
- \[+\infty * \pm\infty = \pm\infty\;,\] \(\phantom{i}\)
- \[+\infty * \pm \lvert a \rvert_{}^{} = \pm \infty\; ,\] \(\phantom{i}\)
- \[(+\infty)^{+\infty} = + \infty\; ,\] \(\phantom{i}\)
- \[(\pm\infty)^{-\infty} = 0\; ,\] \(\phantom{i}\)
- \[\alpha^{+\infty}= +\infty\; ,\] \(\phantom{i}\)
- \[\alpha^{-\infty}= 0\; ,\] \(\phantom{i}\)
- \[\log_{\alpha} (+\infty) = +\infty\; ,\] \(\phantom{i}\)
- \[\log_{\alpha} (0^+) = -\infty\; .\] \(\phantom{i}\)
\(\phantom{i}\)
Definiamo poi alcune forme ambigue, o indeterminate, a cui dovremo prestare particolare attenzione.
\(\phantom{i}\)
- \[\boxed{\frac{0}{0}}\] \(\phantom{i}\)
- \[\boxed{\frac{\pm \infty}{\pm \infty}}\] \(\phantom{i}\)
- \[\boxed{0 * (\pm \infty)}\] \(\phantom{i}\)
- \[\boxed{+\infty -\infty}\] \(\phantom{i}\)
- \[\boxed{0^0}\] \(\phantom{i}\)
- \[\boxed{1^{\pm \infty}}\] \(\phantom{i}\)
- \[\boxed{(\pm\infty)^0}\] \(\phantom{i}\)
\(\phantom{i}\)
Ogni volta che si incontra una forma indeterminata, non si è in grado di stabilire a priori quale sia il valore del limite; sarà necessario effettuare un'indagine più approfondita.
I simboli \(0^+\) e \(0^-\) vanno interpretati come segue. Se \((a_n)_{n\in \mathbb{N}}\) è una successione tale che: esiste \(N\in \mathbb{N}\) tale che \(\forall n\geq N\), \(a_n\geq 0\), e \(\lim_{n\to \infty} a_n=0\) allora diremo che \[\lim_{n\to \infty} a_n = 0^{+}\; .\] Se invece : esiste \(N\in \mathbb{N}\) tale che \(\forall n\geq N\), \(a_n\leq 0\), e \(\lim_{n\to \infty} a_n=0\) allora diremo che \[\lim_{n\to \infty} a_n = 0^{-}\; .\] È utile tenere traccia della positività o negatività della successione convergente a zero quando si devono combinare i limiti.
Tenendo a mente ciò, si ottiene il seguente risultato (che non dimostreremo).
Siano \((a_n)_{n\in \mathbb{N}}\) e \((b_{n})_{n\in \mathbb{N}}\), con limiti rispettivamente \(a\) e \(b\), che possono essere numeri reali, oppure \(\pm \infty\).
Allora si hanno le seguenti uguaglianze: sia \(\alpha > 1\), allora
- \[\lim_{n\to \infty} a_n \pm b_n = a \pm b \; ;\]
- \[\lim_{n\to \infty} a_n b_n = ab\; ;\]
- \[\lim_{n\to \infty} \frac{a_n}{b_n}= \frac{a}{b}\; ; \]
- \[\lim_{n\to \infty} \alpha^{a_n}= \alpha^{a}\; ;\]
- \[\lim_{n\to \infty} \log_{\alpha} (a_n) = \log_{\alpha} (a) \; .\]
Come già accennato sopra, se il membro di destra di una delle uguaglianze del teorema risulta in una forma indeterminata, allora il teorema non dà un'informazione definitiva: il valore del limite va trovato con un'analisi più approfondita.
Abbiamo già dimostrato o discusso i seguenti limiti, che d'ora in poi prenderemo come assodati: sia \(\lambda\in \mathbb{R}\) un numero reale, \(\alpha > 0 \), allora
\begin{align*} n^{\alpha}&\underset{n\to \infty}{\longrightarrow} +\infty \; ,\\ \frac{1}{n^{\alpha}}&\underset{n\to \infty}{\longrightarrow} 0\; ,\\ \lambda&\underset{n\to \infty}{\longrightarrow} \lambda \; . \end{align*}Ora possiamo combinare i limiti qui sopra con le regole fornite dal Teorema 4.3.3 per studiare il limite di quozienti di polinomi di \(n\). Ad esempio, consideriamo \[ a_n= \frac{3n^2+4n+6}{n^3+1}\; . \] Ne consegue che il numeratore \(3n^2+4n+6 \to +\infty +\infty +6=+\infty\), e il denominatore \(n^3+1\to +\infty+1=+\infty\). Siamo quindi di fronte ad una forma indeterminata del tipo \(\frac{+ \infty}{+ \infty}\). Possiamo però risolvere tale indeterminatezza in maniera piuttosto semplice. L'idea, che poi estenderemo a quozienti di polinomi generici, è la seguente: raccogliamo a fattore comune, sia al numeratore che al denominatore, la potenza di \(n\) di grado massimo, in questo caso \(n^2\) al numeratore e \(n^3\) al denominatore: \[ \frac{3n^2+4n+6}{n^3+1}= \frac{n^2\bigl(3+ \tfrac{4}{n}+\tfrac{6}{n^2}\bigr)}{n^3\bigl(1+\tfrac{1}{n^3}\bigr)}= \frac{\bigl(3+ \tfrac{4}{n}+\tfrac{6}{n^2}\bigr)}{n\bigl(1+\tfrac{1}{n^3}\bigr)}\; . \] Ora il numeratore \(3+ \tfrac{4}{n}+\tfrac{6}{n^2}\to 3+0+0=3\), il secondo fattore del denominatore \(1+\tfrac{1}{n^3}\to 1+0=1\), mentre il primo fattore del denominatore \(n \to + \infty \). Combinando i limiti abbiamo quindi che \(\frac{\bigl(3+ \tfrac{4}{n}+\tfrac{6}{n^2}\bigr)}{n\bigl(1+\tfrac{1}{n^3}\bigr)}\to \frac{3}{+\infty}= 0\). Risulta quindi che \[ \lim_{n\to \infty}\frac{3n^2+4n+6}{n^3+1} = 0 \; .\] Analogamente, \[ \lim_{n\to \infty}\frac{\pm8n^{4}+7n^5+6n}{n^\pi+27\pi^2} = \pm\infty\; ,\] e \[ \lim_{n\to \infty}\frac{7n^5+8n^{4}+6n}{2n^5+2} = \frac{7}{2}\; .\]
Abbiamo perciò il seguente conveniente criterio operativo per calcolare il limite di quozienti di polinomi:
- Individuiamo il grado più alto di \(n\) sia al numeratore che al denominatore;
- Confrontiamo tra loro tali gradi più alti (chiamiamoli \(g_{\rm n}\) e \(g_{\rm d}\)): avremo necessariamente o \(g_{\rm n} > g_{\rm d}\), o \(g_{\rm n} < g_{\rm d}\), o \(g_{\rm n}=g_{\rm d}\);
- Se \(g_{\rm n} > g_{\rm d}\), allora il limite è \(\pm \infty\), con il segno determinato dal segno del rapporto dei coefficienti di grado massimo di numeratore e denominatore;
- Se \(g_{\rm n} < g_{\rm d}\), allora il limite è \(0\);
- Se \(g_{\rm n}= g_{\rm d}\), allora il limite è il rapporto fra i coefficienti di grado massimo di numeratore e denominatore.
Note a piè di pagina:
Come per naturali e interi, la relazione d'ordine \(\leq \) è totale in \(\mathbb{Q}\), ovvero dati due numeri razionali \(p,q\), o si ha \(p\leq q\), oppure \(q\leq p\).
Ma questo sappiamo essere vero.
Definiamo massimo di un insieme di numeri \(S\) il numero \(M\in S\) tale che \((\forall s\in S) s\leq M\).
Definiamo il fattoriale \(n!\) di un numero naturale \(n\in \mathbb{N}\) ricorsivamente nel modo seguente:
- \(0!=1\);
- \((n+1)!= n! * (n+1)\).
In altre parole, per ogni \(n>0\), \(n!= 1* 2 * \dotsm * n\).
Due numeri naturali si dicono coprimi se la loro decomposizione in fattori primi non ha fattori comuni.
Il massimo di un insieme di numeri reali \(S\subseteq \mathbb{R}\) è il numero \(M\in S\), se esiste, tale che \((\forall s\in S)\, M\geq s \). Il massimo esiste sempre in insiemi finiti di numeri, ma può non esistere in insiemi infiniti (ad esempio, non esiste il massimo di \(\mathbb{R}\), o di \( ] 0,1 [ \); però esiste il massimo dell'intervallo chiuso \([0,1]\)).
Denotiamo con \(a\), \(\lceil a \rceil \in \mathbb{R}\), il più piccolo numero naturale più grande di \(a\).
Assumiamo che il lettore sia sufficientemente familiare con la definizione di logaritmo, e con le sue proprietà.
Ricordiamo che il modulo soddisfa le seguenti proprietà:
\begin{align*} &\lvert a \rvert_{}^{}= \lvert -a \rvert_{}^{} \\ &\lvert a \rvert_{}^{}\geq 0\\ &\lvert a \rvert_{}^{}=0 \,\longleftrightarrow\, a=0\\ &\lvert \lambda a \rvert_{}^{}=\lvert \lambda \rvert_{}^{} * \lvert a \rvert_{}^{}\\ &\lvert a+b \rvert_{}^{}\leq \lvert a \rvert_{}^{}+ \lvert b \rvert_{}^{} \end{align*}