Geometria secondo Klein

torna a GE 220

La geometria studia le proprietà e le relazioni tra figure nello spazio; il concetto fondamentale, per lo studio e il confronto tra figure, è quello di "uguaglianza". Tale concetto, tuttavia, dipende sensibilmente dal tipo di spazio che stiamo considerando o, più precisamente, dal tipo di trasformazioni tra figure che consideriamo ammissibili per stabilirne l'uguaglianza.

Questa idea è alla base del cosiddetto "programma di Erlangen" proposto dal matematico Felix Klein nel 1872. Egli, per mettere ordine tra i diversi filoni di ricerca in geometria esistenti all'epoca, propose di considerare la geometria come lo studio delle proprietà delle figure che non cambiano rispetto a un certo insieme di trasformazioni considerate ammissibili. La scelta delle trasformazioni considerate ammissibili è arbitraria (a patto di soddisfare alcuni assiomi) e determina precisamente il tipo di geometria con cui stiamo lavorando.

Formalmente: dato un insieme non vuoto S, chiamato spazio, e un gruppo G di trasformazionni su S, la G-geometria su S è lo studio delle figure (sottoinsiemi) di S a meno della relazione di equivalenza ˜ definita come segue:

Nella pratica, alcuni gruppi di trasformazioni ammissibili sono spesso considerati e danno luogo alle geometrie comunemente note.

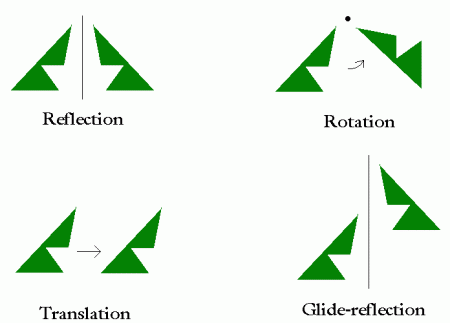
• Geometria metrica: studia le proprietà inviarianti rispetto al gruppo delle isometrie, ovvero le trasformazioni che preservano la distanza tra punti. Per fare ciò è necessario definire sullo spazio una distanza (o metrica) che soddisfi determinati assiomi. Un esempio classico è dato dallo spazio euclideo, i.e. lo spazio vettoriale ${\mathbb R}^n$ dotato della metrica euclidea (o pitagorica) standard.
  
  Esempi di trasformazioni isometriche in dimensione 2:
  
  
  
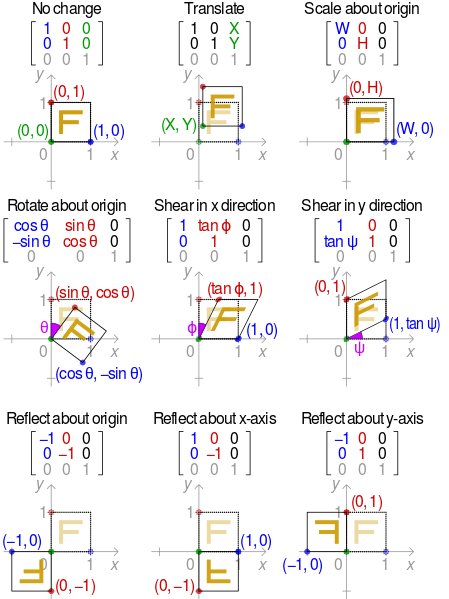
• Geometria affine: studia le proprietà inviarianti rispetto al gruppo delle affinità, ovvero le trasformazioni che conservano il parallelismo. Definire il concetto di parallelismo corrisponde esattamente a definire sull'insieme considerato una struttura di spazio affine; scelto arbitrariamente un punto nello spazio, ciò significa assegnare una struttura di spazio vettoriale. Le trasformazioni ammissibili risulteranno essere quindi le trasformazioni lineari (traslazioni e rotomotetie).
  
  Esempi di trasformazioni affini in ${\mathbb A}_{\mathbb R}^2$, descritte tramite matrici:
  
  
  
• Geometria proiettiva: studia le proprietà inviarianti rispetto al gruppo delle proiettività (o omografie), ovvero le trasformazioni che preservano i birapporti tra punti. Lo spazio più naturale in cui considerare tali trasformazioni è lo spazio proiettivo, ottenuto aggiungendo allo spazio affine un iperpiano, detto iperpiano all'infinito.
  
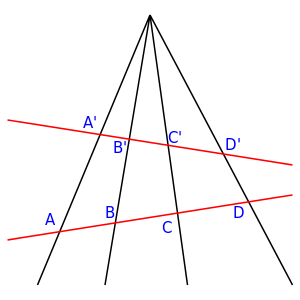
  Un esempio di trasformazione proiettiva in ${\mathbb P}^2$: la figura $\{A,B,C,D\}$ è mappata in $\{A',B',C',D'\}$
  
  
  
• Topologia: studia le proprietà inviarianti rispetto al gruppo degli omeomorfismi, ovvero le trasformazioni che preservano semplicemente la continuità (o "vicinanza") tra punti; un omeomorfismo può essere pensato quindi come una qualunque trasformazione che "deformi" le figure senza creare tagli nè buchi. Il concetto di "vicinanza" tra i punti di un determinato insieme è dato formalmente dalla definizione di una "topologia" sull'insieme stesso, cioè il dato di alcuni sottoinsiemi (definiti "aperti della topologia") che soddisfino determinate proprietà.
  
  Un esempio di omeomorfismo topologico: la superficie di una ciambella può essere deformata nella superficie di una tazza senza operare né tagli né buchi