Figure 1 e 2
L'utilizzo di semplici operazioni di "taglia e cuci" su spazi topologici definiti nello spazio euclideo può portare alla costruzione di nuovi spazi, che presentano proprietà interessanti e talvolta controintuitive.
Le operazioni di "cucitura" (o incollamento) corrispondono formalmente al fatto di considerare il quoziente topologico rispetto a relazioni di equivalenza che associno tra loro i punti che devono essere "cuciti" o incollati. Poichè la definizione di tale relazione di equivalenza non è soggetta ai limiti "fisici" che si incontrano incollando oggetti nello spazio tridimensionale, lo spazio risultante può non essere rappresentabile adeguatamente come spazio topologico immerso in $\mathbb{R}^3$.
A livello formale, il nastro di Moebius è ottenuto incollando due lati di un quadrato secondo la relazione di equivalenza che associa i punti di un lato con i punti del lato opposto in modo simmetrico rispetto al centro del quadrato.
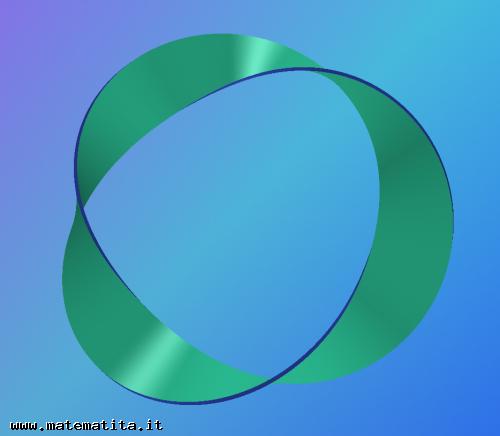
Il risultato è uno spazio che può essere rappresentato in $\mathbb{R}^3$ come un nastro i cui lati corti sono stati incollati dopo aver effettuato una mezza torsione (figura 1) o tre mezze torsioni (figura 2), o un numero dispari qualunque di mezze torsioni: ciò che conta è che i due lati corti del nastro siano incollati antiparallelamente. Si tratta di due rappresentazioni dello stesso spazio topologico intrinsecamente diverse, in quanto non è possibile deformarne una nell'altra all'interno dello spazio euclideo, senza effettuare tagli e reincollamenti.
In termini formali, le due figure rappresentano due sottospazi topologici $X, X' \subset \mathbb{R}^3$, tra loro omeomorfi, che non sono omeomorfi come spazi immersi in $\mathbb{R}^3$, cioè nessuno tra i possibili omeomorfismi $f_X: X \rightarrow X'$ è estendibile a un omeomorfismo $f: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ (Perché? Suggerimento: com'è fatto il bordo delle due figure?).


Figure 1 e 2



Figure 3, 4 e 5
Questo fatto porta con sè la conseguenza che sul nastro di Moebius non è possibile definire i concetti di "destra" e "sinistra": data una coppia di assi cartesiani poggianti sul nastro, al termine di una traslazione completa lungo la superficie ritornerebbe al punto di partenza con un asse "specchiato" rispetto all'altro.
A livello formale, la bottiglia di Klein è ottenuta da un quadrato identificando i lati a due a due, una coppia in modo parallelo, l'altra in modo antiparallelo (figura 6).
Il risultato è uno spazio che non può essere rappresentato fedelmente come sottospazio di $\mathbb{R}^3$, in quanto ogni sua rappresentazione nello spazio euclideo richiede la presenza di un'autointersezione della superficie con sé stessa, che a livello topologico non c'è. I punti di autointersezione della figura 7, infatti, presentano intorni aperti omeomorfi all'unione di due piani incidenti di $\mathbb{R}^3$; mentre nessun punto della bottiglia di Klein definita tramite identificazioni nella figura 6 presenta tale proprietà.
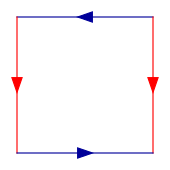
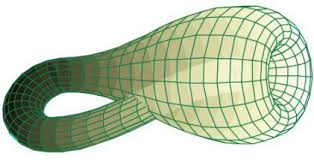
Figure 6 e 7
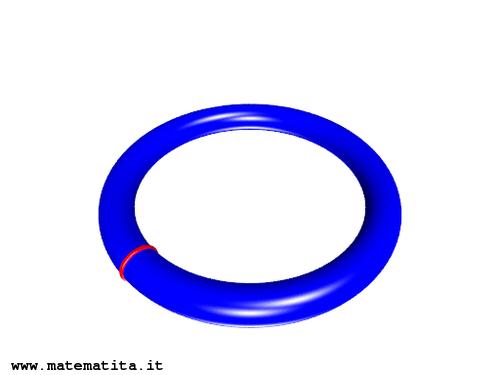
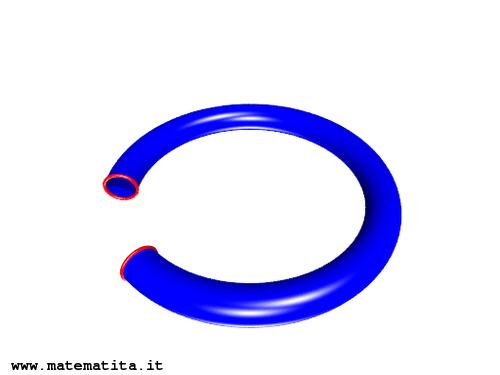
Un altro esempio di figure omeomorfe, non omeomorfe come spazi topologici immersi è dato dalla ciambella (toro) e dalla ciambella annodata. Nelle figure che seguono, il toro è tagliato lungo un meridiano, creando due bordi che vengono reincollati in modo assolutamente identico al termine di una deformazione del resto della figura.
La figura risultante è quindi perfettamente omeomorfa a quella di partenza, in senso astratto: le operazioni di taglio e di reincollamento sono una l'inversa dell'altra mentre la restante deformazione, non coinvolgendo né tagli né buchi, è un omeomorfismo e pertanto topologicamente irrilevante.
Le due figure (quella con il nodo e quella senza) sono invece non omeomorfe come spazi topologici immersi in $\mathbb{R}^3$: nessun omeomorfismo tra i due spazi si estende ad un omeomorfismo di $\mathbb{R}^3$.