General information for the course

• First meeting. The first meeting will be on March 29 at 10:00 AM via Zoom (link will be provided).
• Registration. If you are interested in attending the course, or just to attend the first session to see how it is, please email me at the address below.
• Contact. Email: lucsch at math dot kth dot se
• Level. PhD course.
• Credits. 3.5.
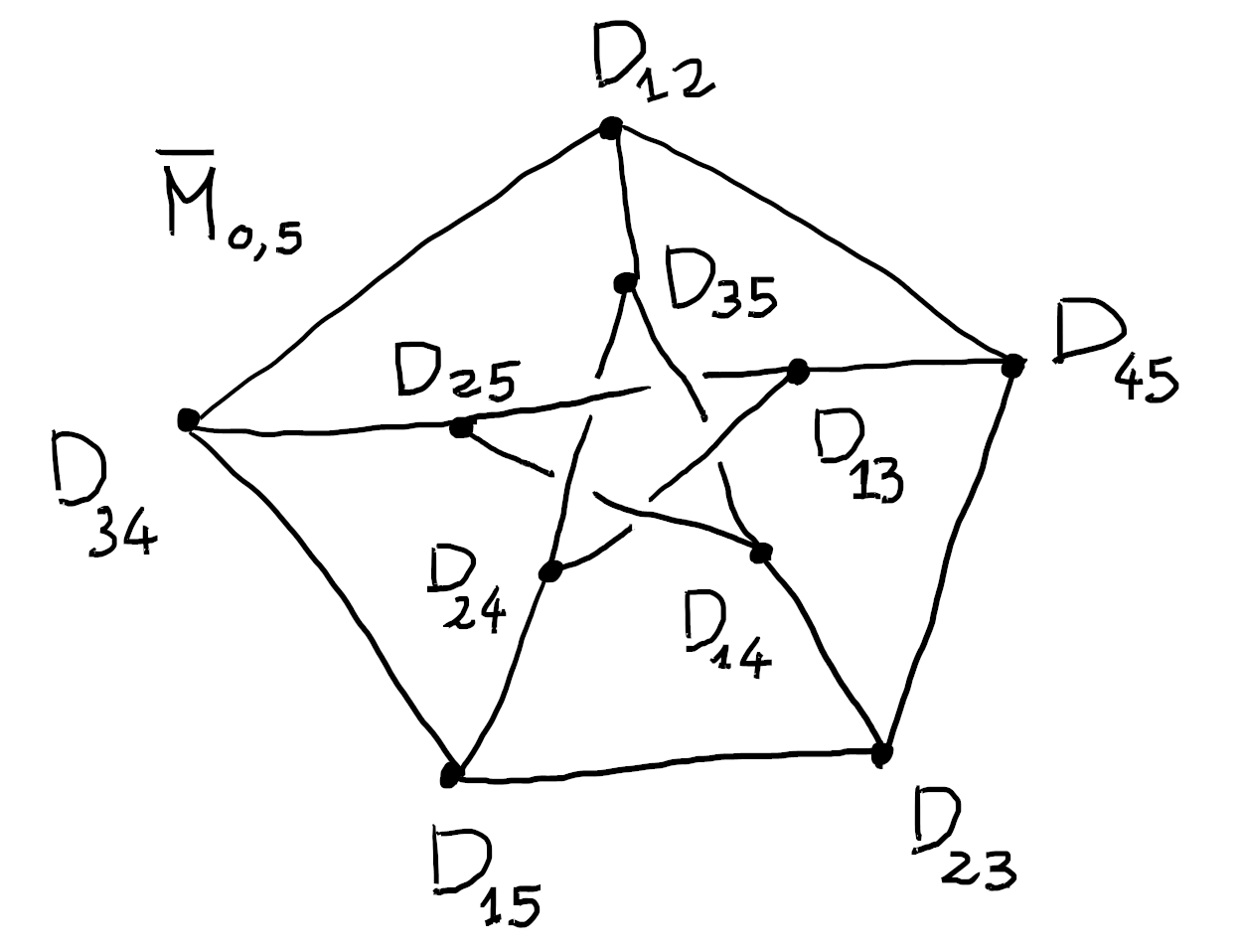
• Intended learning outcomes. The students will learn the basics of intersection theory and moduli theory. These two are then combined to study of the moduli space of stable n-pointed rational curves \(\overline{\mathrm{M}}_{0,n}\). The students will learn about several open problems concerning the structure of the subvarieties of \(\overline{\mathrm{M}}_{0,n}\).
• Rough sketch of content. Part 1: \(k\)-cycles on algebraic varieties. Rational, algebraic, and numerical equivalence among \(k\)-cycles. Pushforward and pullback of \(k\)-cycles. Chow groups. Intersection product and the Chow ring. The real vector space of \(k\)-cycles up to numerical equivalence and the cone of (pseudo)effective \(k\)-cycles. Part 2 Moduli functors, fine and coarse moduli spaces. The moduli space of stable \(n\)-pointed rational curves \(\overline{\mathrm{M}}_{0,n}\). Boundary strata on \(\overline{\mathrm{M}}_{0,n}\) and their intersections. Cones of (pseudo)effective \(k\)-cycles on \(\overline{\mathrm{M}}_{0,n}\). Open problems and recent progress.
• Format of the course. One meeting per week (1 hour and 30 minutes) over Zoom where I will lecture. I will assign a weekly reading assignment which will prepare the students for the next lecture. Occasionally, the weekly reading assignment has the shape of a homework (group work is encouraged as far as solutions are written independently). There will be final 20 minutes presentations on topics chosen by the students. I will provide the list of topics, but I will be happy to consider additional topics suggested by the students. Presentations will be scheduled during exam period 4.
• Type of examination. To pass the course, students will need at least 60% on the occasional homework problems and a passing grade for the presentation at the end of the course.
• Grading scale. pass/fail.
• Prerequisites. A basic introduction to algebraic varieties. I will start by introducing divisors.

Bibliographical references

• David Eisenbud and Joe Harris. 3264 & All That Intersection Theory in Algebraic Geometry.
• Joachim Kock and Israel Vainsencher. An Invitation to Quantum Cohomology: Kontsevich's Formula for Rational Plane Curves. First edition. (KTH library)

• Arnaud Beauville. Complex Algebraic Surfaces, Second edition. (KTH library)
• William Fulton. Intersection Theory. Second edition. (KTH library)

Topics by meeting

• Meeting 1. (29/03/2021) Brief outline of the course, motivation from enumerative geometry, and review of the theory of divisors on smooth algebraic varieties. Lecture notes. Reading assignment: from 3264 book, Sections 1.1, 1.2, 1.3.1. Key concepts from the reading: rational equivalence, Chow group, intersection product, moving lemma, Chow ring, fundamental class.
• Meeting 2. (12/04/2021) Algebraic equivalence of cycles. Lecture notes. Reading assignment: from 3264 book, Sections 1.3.2-1.3.6. Key concepts from the reading: Chow ring of affine space, Mayer-Vietoris and Excision, affine and quasi-affine srtratifications, Chow ring of projective space, pushforward, pullback, projection formula, degree map.
• Meeting 3. (19/04/2021) Numerical equivalence of cycles, basics of vector bundles (needed for reading assignment). Lecture notes. Reading assignment: the last two pages of the lecture notes and from 3264 book, Sections 1.4, 1.4.1, 2.4, 2.4.1, 2.4.2, 2.4.4, 2.4.5, 2.4.6. Key concepts from the reading: Canonical class, canonical class of projective space, genus formula for curves on a surface, blow up of a surface, canonical class of the blow up of a surface.
• Meeting 4. (26/04/2021) Relation with singular homology, Borel-Moore homology, HI spaces. Lecture notes.
• Meeting 5. (03/05/2021) Cones of effective k-cycles, examples of cones of curves on algebraic surfaces. Lecture notes. Reading assignment: Chapter 0 of An invitation to quantum cohomology. Key concepts from the reading: category, functor, natural transformation, representable functor, moduli functor, fine moduli space, universal family, coarse moduli space.
• Meeting 6. (10/05/2021) Cone of curves of the blow up of \(\mathbb{P}^2\) at the nine base points of a pencil of cubics, \(n\)-pointed smooth rational curves, the fine moduli space \(\mathrm{M}_{0,n}\) and the universal family. Lecture notes. The list of topics for final presentation and the due dates can be found here.
• Meeting 7. (17/05/2021) Stable \(n\)-pointed rational curves, the fine moduli space \(\overline{\mathrm{M}}_{0,n}\), forgetful morphisms, universal family, Kapranov's blow up construction. Lecture notes.
• Meeting 8. (24/05/2021) Students' presentations. Here you can find some additional conclusive notes about the boundary of \(\overline{\mathrm{M}}_{0,n}\) and cones of effective cycles.

List of topics for final presentations

• Topic: Numerical criteria for ampleness and examples. Presented by: Simon Cooper.
• Topic: The Naruki compactification of the moduli space of marked cubic surfaces. Presented by: Lukas Gustafsson.
• Topic: The circles of Apollonius. Presented by: Erik Lindell.
• Topic: Introduction to stacks. Presented by: Stefan Reppen.